UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 6.2.6
Seja a região infinita delimitada pelas curvas e , . Calcule o volume do sólido obtido pela rotação de em torno do eixo .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume de rotação, em torno do eixo , da região limitada pelas curvas e , . Mas que região é essa? Vamos dar uma olhadinha no gráfico:
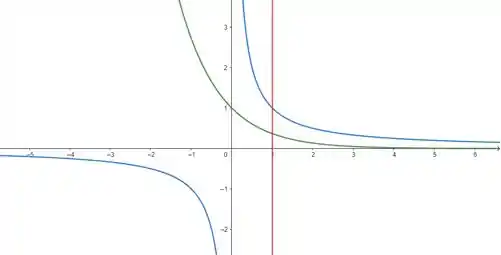
Nossa região é toda a aréa depois dessa reta em vermelho, que é a reta . Então, nós temos uma região infinita, o que significa que nosso limite de integração vai de até . Além disso, a gente precisa lembrar que nosso volume de rotação é dado pela integral da área dos infinitos anéis formados na nossa região, que tem um raio externo e um raio interno , ou seja:
Assim, substituindo os dados do enunciado, conseguimos obter o volume do sólido gerado.
Vamos lá!
Passo 2
Sabendo que e , no intervalo , vamos ter:
Integrando, usando a regrinha da potência, temos:
Para o limite superior, precisamos calcular o limite de quando . No limite inferior, apenas substituímos . Fica assim:
Quando , vamos ter . Então, nosso resultado será:
Valeu, galera! Até a próxima! 😉