USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 7m
Para as funções cujas leis são dadas abaixo, verifique se são limitadas em seu domínio de definição. Caso não seja limitada, verifique por qual sequência de pontos ela cresce (ou decresce) arbitrariamente:
m)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar se a função que ele nos deu é limitada em seu domínio. Tá, mas o que é uma função limitada mesmo?
Uma função é dita limitada, em seu domínio, quando sua imagem está contida em um intervalo, ou seja, , onde . Também podemos definir uma função limitada quando existe um valor finito tal que para qualquer valor de e .
Então, vamos analisar nossa função com base nessa definição. Se não for possível encontrar esse valor que limita nossa função, ou esse intervalo , o enunciado pediu pra gente verificar onde a função é crescente ou decrescente definindo alguns pontos arbitrários.
Vamos lá!
Passo 2
Nossa função é dada por:
Pra verificar se existe um número que limita a nossa função, vamos verificar o que acontece com ela quando e vão pra infinito, calculando o limite:
Pra facilitar nas contas, vamos usar as coordenadas polares na forma:
Assim, temos:
Usando a identidade , vamos ter:
Simplificando:
Como o limite não depende de , temos:
Mas a função cosseno é sempre limitada no intervalo , para qualquer valor de . Portanto, podemos dizer que nossa função também é limitada. Isso pode ser visto melhor no gráfico abaixo:
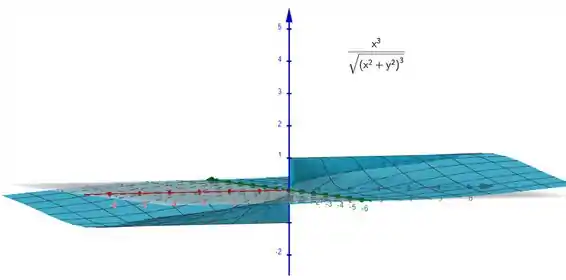
Valeu, galera! Até a próxima! 😉