Lista 2– Universidade UFABC– questão 12
Seja:
- Verifique que as curvas com , são curvas de n��vel de f.
- É possível definir f na origem de modo a torná-la contínua? Justifique.
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Para determinar uma curva de nível, vamos substituir a função y na função e determinar o gráfico da função como uma curva de nível. Bora lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim:
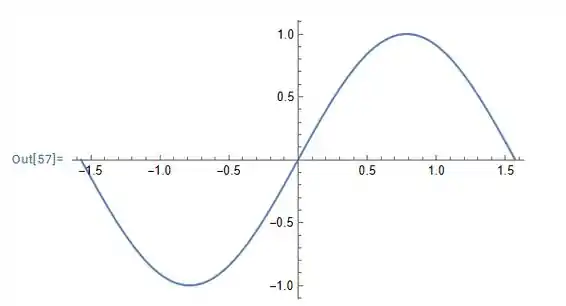
Se “a” varia de , temos o seguinte gráfico:
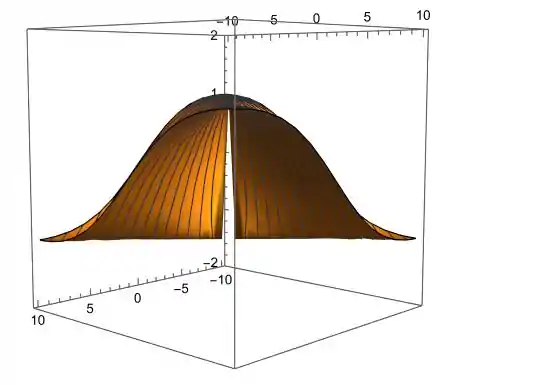
E o gráfico da função já calculada como curva de nível é:
Lateralmente:
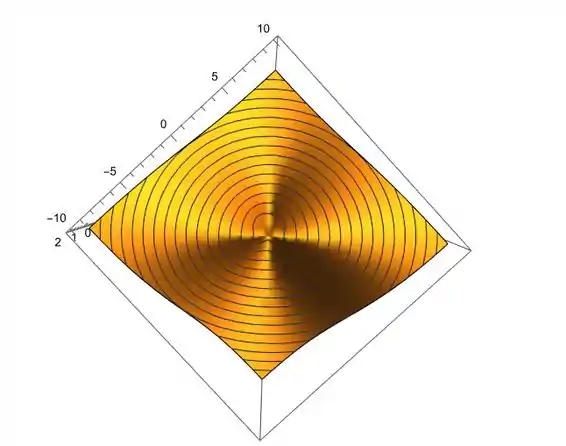
Visão superior:
E uma visão superior num ângulo qualquer:
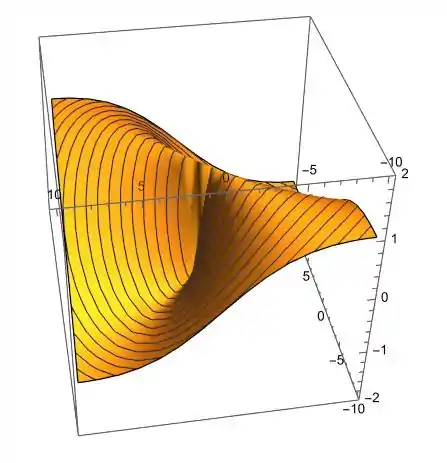
As linhas do gráfico já são as curvas de níveis.
Veja por exemplo que se a é igual a função vai para z, e é uma curva de nível. Como visto na visão lateral, há uma curva de nível em k=0, e isso pros demais valores no intervalo de a, visto que é só uma reta que varia em x e y, não alterando no eixo z. Veja para ajudar:
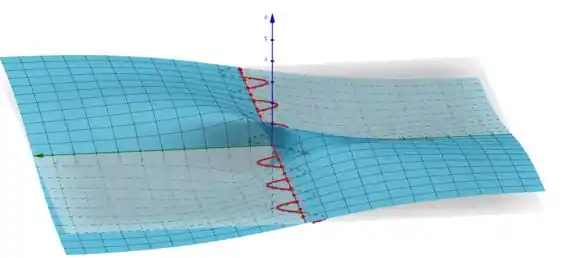
Caso se interesse, os primeiros gráficos foram produzidos com o software Wolfram Mathematica, e o segundo com o Geogebra.
Passo 3
Para b:
Se f(x,y) for continua na origem, então ela existe no limite onde , então:
Por ser um limite duplo, podemos usar o teorema de que se cada um dos limites x e y derem o mesmo valor na sua limitação, se forem iguais então o limite existe no ponto, caso ele seja diferente, o limite não existe. Vamos lá:
E o mesmo para y, assim, ela so seriam iguais de x e y fossem iguais. Como x e y são 0, então ficaria e assim diverge.
Resposta
B) não, ela diverge.