UFABC. Cálculo. Funções de Várias Variáveis. Lista 2. Questão 4e.
4- Esboce o maior conjunto no qual a função é contínua:
e)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Para essa questão, foi dada a função
Com base nessa equação, temos que definir qual é o maior conjunto de valores que é contínua.
Mas que negócio é esse??! 🤔🤔
Determinar o maior conjunto no qual a função é continua é um pouco parecida com determinar o domínio de uma função .
No caso, temos que encontrar os valores que quando substituímos em fazem a questão ser indefinida.
Por exemplo, no nosso caso, lembra como é o gráfico de ?
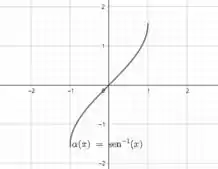
Vemos que a função é definida no intervalo .
Mas e no caso de uma função tridimensional, como se faz?
Passo 2
Na nossa função a ideia é praticamente a mesma.
Para ser definida, dentro do deve estar dentro do intervalo .
Por curiosidade, vamos ver como é o gráfico de ?
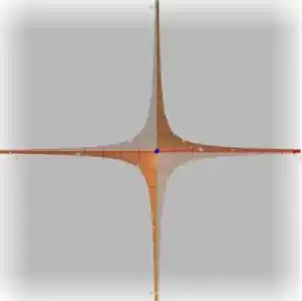
Vendo de cima, podemos ver que a função é definida quando o produto estiver dentro do intervalo .
A forma mais geral de se dizer isso é que se temos , . Ou seja,
Passo 3
Com base nas afirmações que construímos anteriormente, vemos que a função é contínua apenas quando o produto estiver dentro do intervalo .
A forma mais didática de escrever isso é
E fim! Iae, o que achou? Responde Aí! 😁
