UFABC. Cálculo. Funções de Várias Variáveis. Lista 2. Questão 4d.
4- Esboce o maior conjunto no qual a função é contínua:
d)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, temos que determinar qual o maior conjunto no qual a função é contínua. Mas peraí, o que isso significa? 🤔
Dizer qual é o maior conjunto no qual a função é contínua é dizer quais são os conjuntos de valores possíveis para , algo um pouco parecido com o domínio da função.
Neste caso temos uma função dada por:
Você lembra como é o gráfico de ?
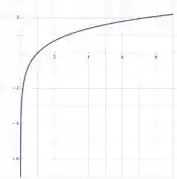
Vemos que é definido quando .
Então a principal ideia dessa questão é dizer para quais valores de é definida.
Bora lá!
Passo 2
Como vemos antes é definida quando , trazendo essa informação para nosso probleminha, temos que é definida quando
Organizando de forma mais matemática essa ideia, temos
Vemos que essa inequação é muito parecida com a equação da circunferência, onde
No caso, como nossa função é definida em , ou seja, para pontos de de raio maior que a partir do eixo , a função não será definida quando .
Passo 3
Com base nas afirmações que construímos anteriormente, vemos que a função é contínua apenas fora da circunferência .
A forma mais didática de escrever isso é
Só por curiosidade, vamos ver o gráfico de ?
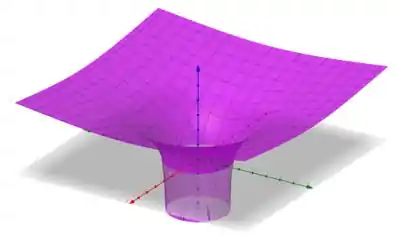
Podemos ver de forma mais física que a função é indefinida dentro da circunferência que encontramos.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
