USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 20c
Descreva os pontos onde é contínua. Faça também o esboço do domínio :
(c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente definir onde a função é contínua e esboçar o domínio da função.
Mas o conjunto no qual uma função é contínua é seu próprio domínio. E pra encontrar esse domínio, temos que verificar as restrições da função, ou seja, os valores para os quais ela não existe.
Só precisamos nos lembrar que, basicamente, todas as funções mais clássicas, como as polinomiais, trigonométricas, exponenciais e logarítmicas, são contínuas nos seus domínios. Inclusive, quando fazemos composições com essas funções, beleza?
Então, vamos lá descobrir o domínio dessa função e plotá-lo no plano cartesiano.
Passo 2
Nossa função é dada por:
Repare que temos uma função trigonométrica, que é contínua em todo seu domínio. E no argumento da função temos uma raiz. E aí a única restrição que nós temos é de que o que está dentro da raiz seja positivo (porque temos uma raiz de índice par). Assim, podemos escrever a restrição:
Passando a constante pro outro lado:
Multiplicando ambos os lados por e invertendo o sinal da desigualdade, temos:
Portanto, nossa função é contínua no domínio:
Esboçando isso no plano cartesiano, teremos:
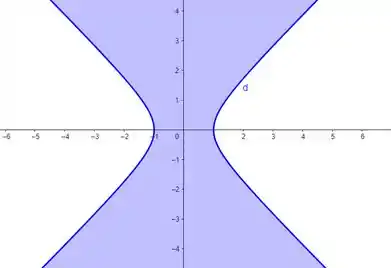
Valeu, galera! Até a próxima! 😉