Considere a função
a) Determine o valor de para que a função seja contínua no ponto (0,2);
b) Faça o esboço do gráfico de para encontrado no item
c) Mostre que não existe
d) A função é diferenciável em
Passo 1
a) Vamos começar isso aqui. A questão nos pergunta o valor de para que a função seja contínua no ponto . Ou seja, vamos calcular esse limite com
Observe que a função quando se aproxima de dentro da região ela vale , e que deve ser o resultado do nosso limite acima, logo
Passo 2
b) Para o esboço do gráfico temos que quando teremos , ou seja, um disco com raio variando ontre 2 e 4.
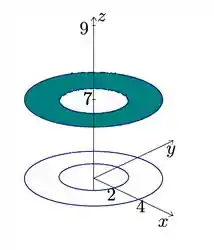
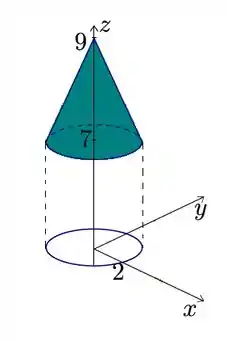
Já quando é o nosso cone. Mas lembra que ele está restrito dentro da circunferencia no plano xy.
Uma continha rápida pra gente ver onde fica o pico desse cone, seria ond eo ponto são iguais a zero
Ou seja
Atenção a restrição de xy. Juntando então tudo temos
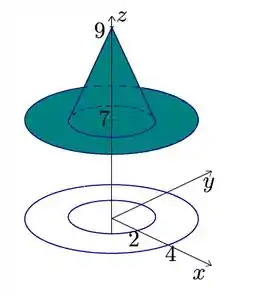
Passo 3
c) essa letra agora nos pede pra mostrar que não existe Bom, pra fazer isso vamos precisar considerar com
Lembra que pela definição da derivada parcial, onde fazemos a coordenada , a existência de vai ser igual à de .
Com entre 2 e 4 temos . Então (quando entre 2 e 4). Então Para existir, deve ser igual a . Vamos conferir isso
Temos então que , então não existe.
Passo 4
d) Próxima coisa que ele nos pergunta é se a função é diferenciável em , que a resposta é NÃO, afial de contas nem mesmo existe como provamos anteriormente.
Resposta
.
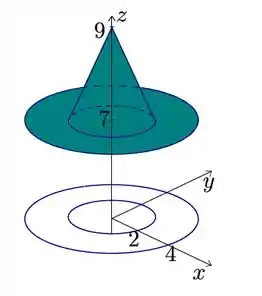
.
.