Assinale (VERDADEIRO) ou F (FALSO). Se VERDADEIRO, justifique sua resposta, se FALSO, apresente uma função que satisfaça tal propriedade.

() Se for uma função contínua no ponto , então é derivável em .

() Se for uma função derivável no ponto , então é contínua em .

() Se existe, então .

Vamos trabalhar as duas primeiras alternativas em conjunto, note que a primeira afirmação é FALSA, e a segunda é VERDADEIRA. Uma função contínua não é derivável necessariamente, por exemplo, a função módulo

ela tem como gráfico

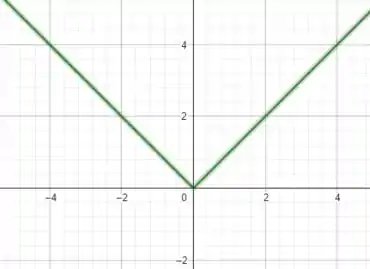
ou seja, é claramente contínua em , no entanto, pela definição de derivada, temos que

é derivada em , no entanto, pela definição de módulo, temos que os limites laterais tomam a seguinte forma

e

ou seja, os limites laterais são diferentes, indicando que o limite não existe! Sendo assim, uma função contínua não necessariamente é derivável!

No entanto, como vimos anteriormente, temos que uma função é derivável em um ponto se

existe e é finito! Pois essa é a inclinação de uma reta tangente a nossa função! Note que só é possível haver uma reta tangente se a função for contínua! Se houver uma descontinuidade em , teríamos que o nosso limite não existiria ou seria infinito! Falta apenas uma afirmativa, que pede para avaliarmos a afirmação

Se existe, então

novamente, está dizendo, se a função é diferenciável em , ela é contínua, pois

é a definição de continuidade! Sendo assim, como discutimos anteriormente, a afirmação é VERDADEIRA! A questão foi isso! Te vejo na próxima! Tchau Tchau!