Lista 5 – 2020 – UFAM – Cálculo I – Questão 1
(Stewart) Usando um aplicativo para construir gráficos de funções, dê zoom em direção aos pontos , e sobre o gráfico da função . O que você observa? Explique o que você viu em termos da diferenciabilidade da função .
Passo 1
Falaeee, beleza??? Antes de tudo, vamos começar plotando o gráfico e ver os pontos que a questão nos disse. Se liga:
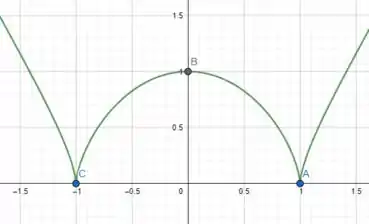
Passo 2
No ponto B a gente vê que a função é diferenciável pois se a gente aumentar o zoom, a curva cada vez mais irá aparentar uma linha reta. Olha:
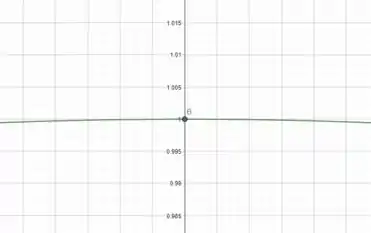
Passo 3
Já nos pontos A e B, embora a gente aumente esse zoom, a curva jamais irá se aproximar de uma reta. Ela sempre mostrará aquele “bico”. Ou seja, nos pontos A e C ela não será diferenciável.
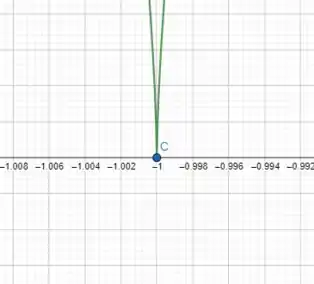
Tranquilo? Responde Aí!! ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você
Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de
Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .
Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .
Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .