UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - 1ª Lista - 2023.1, Questão 12
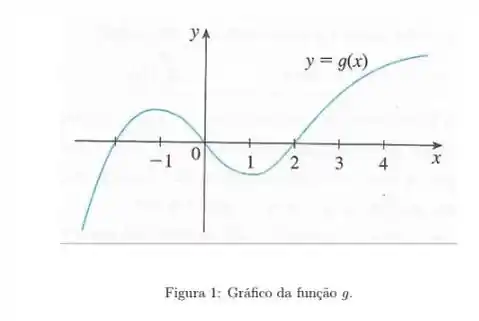
Escreva na ordem crescente os números e .
Passo 1
Vamos primeiro calcular as derivadas nos pontos especificados e depois organizá-las em ordem crescente.
Dada a função , vamos calcular as derivadas nos pontos dados:Para :
Passo 2
Passo 3
Resposta
Portanto, os valores das derivadas e em ordem crescente são: -4, 0, 16, 18, 62 .
Exercícios de Livros Relacionados
Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você
Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de
Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .
Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .
Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .