Considere a função
Esboce o gráfico de .
Determine analiticamente o(s) ponto(s) em que é descontínua.
Esta(s) descontinuidade(s) pode(m) ser removida(s)? Justifique.
A função é diferenciável em ? Justifique.
Passo 1
Para esboçarmos o gráfico é bom que a gente primeiro esmiúce esse módulo aí que aparece na função. Pela definição, olhando só para sua parte do numerador, ficaria assim:
Quer dizer, quando o que está dentro do módulo é positivo, o termo vale exatamente o que está no módulo, quando é negativo vale o módulo vezes .
Juntando a isso o fato de que o pedaço está todo dividido por , a ficaria assim:
Agora sim, muito mais simples de visualizar o gráfico.
Passo 2
Desenhamos a que concluímos no último passo:
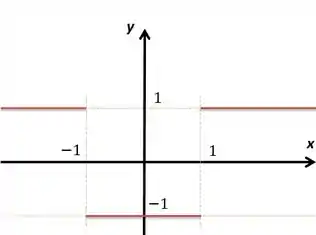
Passo 3
Concluímos na letra que o valor de seria
Cujo gráfico seria
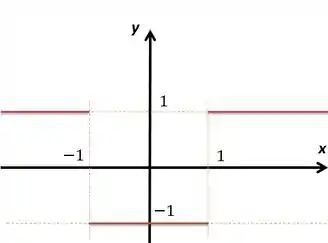
Concluímos por esse gráfico analiticamente, como pede a questão, que os pontos onde há saltos no gráfico e, portanto, descontinuidades são onde e onde .
Passo 4
Temos a seguinte função:
Se a função tem seus limites laterais iguais porém o valor da função no ponto inexiste ou é diferente desses limites, dizemos que essa é uma descontinuidade removível. Melhorando, uma descontinuidade em é removível se:
Para e os limites laterais não são iguais, o que faz com que essas duas descontinuidades não sejam removíveis, como podemos calcular:
Conclusão, não podem ser removidas
Passo 5
Para ser diferenciável a função deve ser contínua; como não é contínua em concluímos que ela também não é diferenciável nesse ponto.