Exercícios Resolvidos de Diferenciabilidade

Ver Teoria

Exercício 81 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - UNICAMP (MA111) - Lista 7, Questão 10a

(10) (a) Prove que se é diferenciável em , então também é diferenciável em desde que .

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema temos que mostrar que se temos uma função que seja diferenciável em , então o modulo de também é diferenciável desde que .

Tem ideia de como fazer isso? 🤔

Vamos analisar a situação e depois demonstrar com um exemplo...

Bora lá! 😉

Passo 2

Bom... temos uma função que é diferenciável. Se fizermos a mesma análise para temos que pensar um pouco mais pois o que pode acontecer é que a função pode ir a e ao invés da função seguir seu caminho convencional, ela “reflete” no eixo e volta para positivo.

O problema é que isso pode ocorrer de forma tão brusca que perde sua diferenciabilidade pois os limites laterais da função divergem do valor real.

Por exemplo, se tivermos uma função

Seu modulo é dado por

Esboçando essas funções no plano cartesiano, temos

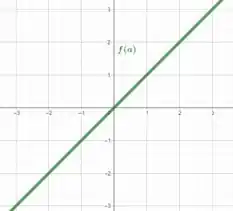
Perceba que no ponto a função não é diferenciável.

Logo, toda função que seja diferenciável, seu módulo também é diferenciável.

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

Toda função que seja diferenciável, seu módulo também é diferenci��vel

Exercícios de Livros Relacionados

Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você

Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de

Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .

Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .

Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .