UFES, Cálculo I, Lista 7, 2018.1, questão 15g
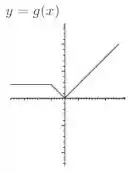
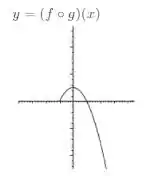
Considere as funções
e
(g) Indique nos gráficos os pontos em que , e não são diferenciáveis
Passo 1
Faaaaala, galeeeera! Como estão, tudo belezinha?
Para obter os pontos onde a função não é diferenciável, basta analisar o domínio. O domínio nada mais é que o conjunto de entradas permitidas na função, ou seja, todos os valores de para os quais a função existe.
Para :
Logo essa função é diferenciável em todos os pontos.
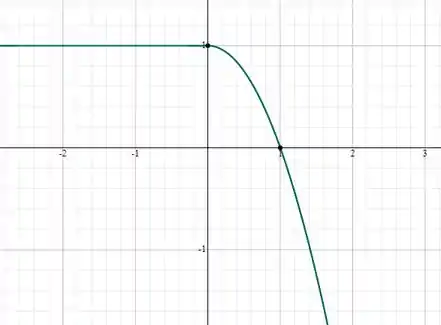
Passo 2
Para :
Logo essa função é diferenciável em todos os pontos.
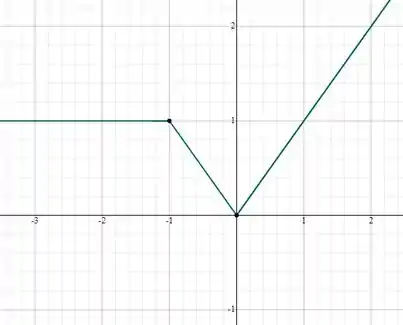
Passo 3
Para :
Logo essa função é diferenciável em todos os pontos.
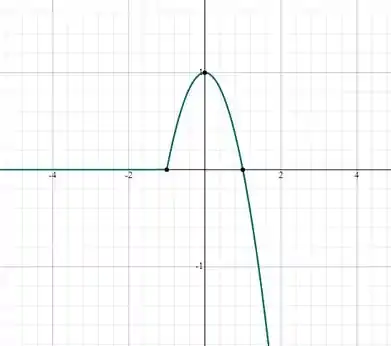
Prontinho! Até mais!
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você
Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de
Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .
Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .
Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .