USP– Cálculo 1 – Lista 5 – Questão 6Parte1
Parte 1: Mostre que não é derivável em e calcule
Parte 2: Esboce o gráfico de
Passo 1
Oi pessoal, tudo bem por aí? Nessa segunda parte vamos fazer o esboço da função!
Já mostramos que ela não é diferenciável, embora seja contínua! Isso porque...
Verificamos a continuidade:
Antes de
Depois de
E também quanto a derivada! Saca só a derivada dessa função:
Ela assume valores iguais em torno de ! E por isso, essa função é diferenciável.
Pela esquerda ela tem cara de parábola, depois passa a ser uma reta!
Então a ideia é usar essas informações para construir o gráfico!
Bora lá!
Passo 2
A função é
Em torno de ela vale ! E a inclinação pelos dois lados é
E organizando essas informações temos:
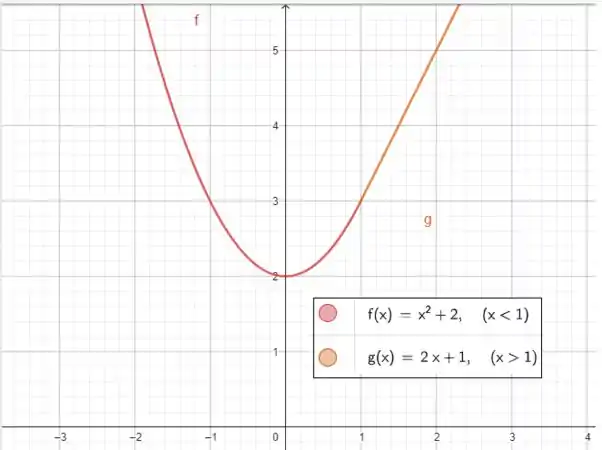
Percebe como em torno do ponto de ‘quebra’ a mudança entre as funções é suave? Isso nos mostra que sim a função é diferenciável! Uma função não diferenciável teria um bico!
beleza?
E é isso! Até a próxima!
Resposta
