5. Mostre que a função não é diferenciável em . Encontre uma fórmula para e esboce seu gráfico.
Passo 1
Oi, galerinha! Tudo bom? Aqui temos que dizer em quais pontos as função não é diferenciavel. E para isso precisamos lembrar quais critérios devem ser atendidos para função ser diferenciavel.
O primeiro é: funções que não são contínuas em um certo ponto, automaticamente, não são diferenciáveis nesse ponto.
Agora, se a função for contínua, ela pode ou não ser diferenciável, precisamos usar outro critério para avaliar: ela precisa ter suas derivadas laterais iguais e diferente de .
Agora vamos analisar a função!
Passo 2
No problema, nós temos uma função modular e ela pode ser escrita dessa forma:
Ou seja, ela possui um comportamento para valores menores que e outro comportamento para valores maiores que .
Sendo assim, precisamos analisar a derivada para cada comportamento e verificar se elas são iguais.
Para , teremos
Já para , teremos
Como,
A derivada não existe.
Passo 3
Agora que temos as derivadas para cada intervalos (maiores e menores que ), é só plotarmos no gráfico as duas retas para representar o gráfico da derivada.
Fica assim:
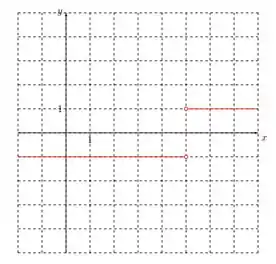
Resposta
No texto.