Introdução às derivadas, continuidade
Decida se a proposição abaixo é falsa ou verdadeira, justificando:
Se não é derivável em , então
Passo 1
Vamos começar tentando entender o que ele está falando ali, ele começou afirmando que a função não é derivável em , e disse que isso faz com que se tenha
A função ser derivável ou não é de boa, mas o que é isso que ele afirmou no final?
Ele quer dizer que o limite da função quando tende a é diferente do valor da função em , isso te lembra alguma coisa?
Quando temos o limite sendo igual ao valor da função isso quer dizer que a função é contínua.
Isso quer dizer que a afirmação dele na verdade é
Se não é derivável em , então ela não é contínua.
Mas isso não é verdade, podemos ter funções que não são deriváveis mas que sejam contínuas em . Um exemplo seria
Essa é a função módulo, podemos escrever essa função assim
Assim o gráfico vai ficar
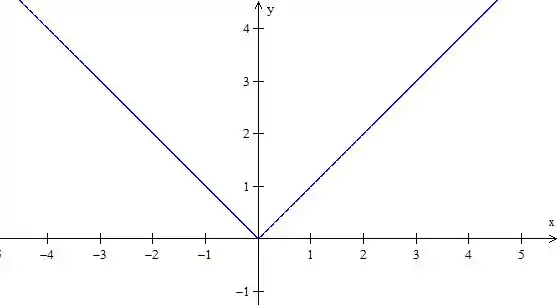
E ela é contínua, mas a sua derivada vai ser
E isso vai dizer que sua derivada em não existe mas ela é contínua, isso é um contra exemplo dessa afirmação
Resposta
Falso