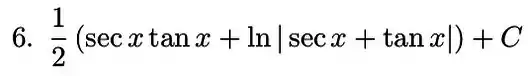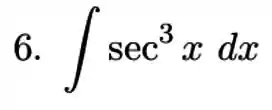
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 100123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

Passo 1

Aqui vamos ter que escolher u   e   d v e fazer algumas manipulações para ficar mais fácil, vamos lá!

u = sec ⁡ x

d v = sec 2 ⁡ x

Então

d u = sec ⁡ x tan ⁡ x   d x

E

v = tan ⁡ x

Passo 2

Agora vamos substituir isso na nossa expressão da integral por partes

∫ u   d v = u v - ∫ v   d u

∫ s e c 3 x d x = sec ⁡ x tan ⁡ x - ∫ tan ⁡ x sec ⁡ x tan ⁡ x   d x

∫ s e c 3 x d x = sec ⁡ x tan ⁡ x - ∫ tan 2 ⁡ x sec ⁡ x   d x

Passo 3

Agora, precisamos lembrar da identidade trigonométrica

tan 2 ⁡ x = sec 2 ⁡ x - 1

Logo

∫ s e c 3 x d x = sec ⁡ x tan ⁡ x - ∫ ( sec 2 ⁡ x - 1 ) sec ⁡ x   d x

∫ s e c 3 x d x = sec ⁡ x tan ⁡ x - ∫ sec 3 ⁡ x d x - ∫ sec ⁡ x   d x

Ahhh que droga ein? Chegamos na mesma ∫ sec 3 ⁡ x   d x que estamos querendo nos livrar. Relaxa! Vamos passar isso pro outro lado da igualdade.

2 ∫ sec 3 ⁡ x d x = sec ⁡ x tan ⁡ x + ∫ sec ⁡ x d x  

Ou seja,

∫ sec 3 ⁡ x d x = 1 2   sec ⁡ x tan ⁡ x + ∫ sec ⁡ x d x  

Passo 4

Sabemos que ∫ sec ⁡ x d x   = ln ⁡ sec ⁡ x + tan ⁡ x (se ficar com dúvida nisso, tá mais detalhado na parte de integrais trigonométricas).

Então

∫ sec 3 ⁡ x d x = 1 2   sec ⁡ x tan ⁡ x + ln ⁡ sec ⁡ x + tan ⁡ x + C

Vê se não esquece de colocar essa constante no final viu?

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x