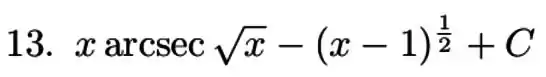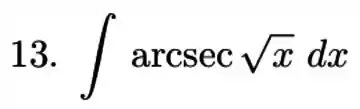
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 701234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Partiu resolver mais uma integral por partes! Mas antes de ir aplicando o que sabemos de integral por partes, vamos facilitar nossa vida e fazer uma substituição aqui, pra ficar um pouco mais claro. Vamos substituir

u = x

d u = 1 2 x d x = 1 2 u d x

Então nossa integral vai ficar

∫ arcsec ⁡ x d x = 2 ∫ u   arcsec ⁡ u   d u

Passo 2

Agora sim ! Ficamos com uma expressão que podemos usar na integração por partes. Cuidado! Não confunda o u   da substituição com o da integração por partes. Pra facilitar vamos chamar o da integração por partes de u 2 .

u 2 = arcsec ⁡ u

d v = u   d u

Então

d u 2 = 1 u   u 2 - 1   d u

v = u 2 2

Passo 3

Pronto! Já encontramos tudo que precisamos na nossa expressão da integral por partes.

∫ u 2   d v = u 2 v - ∫ v   d u 2

2 ∫ u arcsec ⁡ u   d u = 2 arcsec ⁡ u u 2 2   - ∫ u 2 2 1 u   u 2 - 1   d u

2 ∫ u arcsec ⁡ u   d u = u 2 arcsec ⁡ u - ∫ u 2 u 2 - 1 d u

A integral

∫ u 2 u 2 - 1 d u = u 2 - 1

Então

2 ∫ u arcsec ⁡ u   d u = u 2 arcsec ⁡ u - u 2 - 1

Passo 4

Agora falta a gente voltar lá na expressão do passo 1 e desfazer a substituição

u = x

∫ arcsec ⁡ x d x = 2 ∫ u   arcsec ⁡ u   d u

∫ arcsec ⁡ x d x = u 2 arcsec ⁡ u - u 2 - 1

∫ arcsec ⁡ x d x = x arcsec ⁡ x - x - 1

Não podemos esquecer de colocar a constante de integração

∫ arcsec ⁡ x d x = x arcsec ⁡ x - x - 1 + C

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x