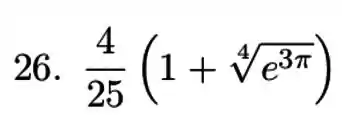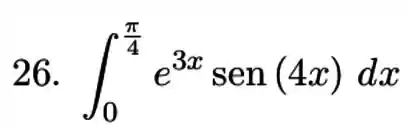
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos lá resolver nossa integral! Tem cara de integral por partes. Para isso precisamos encontrar u e d v . Vamos lembrar do nosso macete para escolher u , o LIATE(logarítmica, inversa trigonométrica, algébrica, trigonométrica e exponencial). No caso da nossa integral

∫ 0 π 4 e 3 x sen ⁡ ( 4 x ) d x

A função trigonométrica tem prioridade de acordo com nosso macete então

u = sen ⁡ 4 x

d v = e 3 x d x

Passo 2

Escolhidos u e v , precisamos encontrar d u e v .

u = sen ⁡ 4 x

d u = 4 cos ⁡ 4 x

E

d v = e 3 x d x

v = e 3 x 3

Agora, com u , d u , v e d v vamos aplicar a regra da integração por artes.

∫ u   d v = u v - ∫ v   d u

Aplicando

∫ e 3 x sen ⁡ 4 x d x = sen ⁡ 4 x e 3 x 3 - ∫ e 3 x 3 4 cos ⁡ 4 x d x

∫ e 3 x sen ⁡ 4 x d x = e 3 x 3 sen ⁡ 4 x - 4 3 ∫ e 3 x cos ⁡ 4 x d x

Passo 3

Perceba que chegamos em outro caso de integração por partes. Usando os mesmos critérios vamos escolher

u 2 = cos ⁡ 4 x

v 2 ' = e 3 x

Então

d u 2 = - 4 sen ⁡ 4 x d x

v 2 = e 3 x 3

Aplicando na integração por partes

∫ e 3 x sen ⁡ 4 x d x = e 3 x 3 sen ⁡ 4 x - 4 3 e 3 x 3 cos ⁡ 4 x - ∫ e 3 x 3 ( - 4 sen ⁡ 4 x ) d x

∫ e 3 x sen ⁡ 4 x d x = e 3 x 3 sen ⁡ 4 x - 4 9 e 3 x cos ⁡ 4 x + 4 9 ∫ e 3 x sen ⁡ 4 x d x

Passo 4

Perceba que chegamos na mesma integral do início, vamos reescrever isso passando ela pro outro lado da nossa integral.

∫ e 3 x sen ⁡ 4 x d x - 4 9 ∫ e 3 x sen ⁡ 4 x d x = e 3 x 3 sen ⁡ 4 x - 4 9 e 3 x cos ⁡ 4 x

25 9 ∫ e 3 x sen ⁡ 4 x d x = e 3 x 3 sen ⁡ 4 x - 4 9 e 3 x cos ⁡ 4 x

Então vamos ficar com

∫ e 3 x sen ⁡ 4 x d x = 3 e 3 x 25 sen ⁡ 4 x - 4 25 e 3 x cos ⁡ 4 x

Passo 5

Aplicando os limites de integração, ficamos com

∫ 0 π 4 e 3 x sen ⁡ 4 x d x = 3 25 e 3 π 4 sen ⁡ ( π ) - 4 25 e 3 π 4 cos ⁡ π - 3 25 e 0 sen ⁡ ( 0 ) - 4 25 e 0 cos ⁡ 0

∫ 0 π 4 e 3 x sen ⁡ 4 x d x = 4 25 e 3 π 4 + 4 25

Rearranjando ficamos com

∫ 0 π 4 e 3 x sen ⁡ 4 x d x = 4 25 e 3 π 4 + 1

Prontinho, resolvido !

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x