Sejam números inteiros. Sabendo que
Determine .
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pediu para descobrir quanto vale os coeficientes . E nos deu essa igualdade aqui:
Então a ideia para resolver é a seguinte: resolver a integral do lado esquerdo, aplicar os limites de integração. Com isso vamos ficar com uma expressão do lado esquerdo e que deve ser igual à expressão do lado direito da equação.
E aí aplicar o conceito de igualdade de equações: um termo só é igual ao outro quando os coeficientes das mesmas partes literais são iguais. Vamos comparar os termos semelhantes
Beleza? Mas relaxa, vou fazer passo a passo com você!
Passo 2
A integral indefinida do lado esquerdo é:
Logo de cara vemos que tem uma função exponencial com um polinômio. Não temos a derivada de uma nem da outra no integrando, então não podemos usar a técnica da substituição simples. O que nos resta? POR PARTES!
Relembrando a técnica de integração...
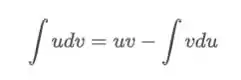
Mas qual função escolher para ? E para ? Se você não sabe qual escolher para , você pode usar o LIATE:

Assim vamos escolher e . Daí temos:
Agora é só substituir na fórmula de partes:
Beleza?

Passo 3
Agora vamos aplicar nos limites de integração:
Tranquilo até aqui?

Passo 4
Agora para determinar os coeficientes, precisamos voltar à igualdade que o problema nos deu:
E comparar com o resultado da integral definida que encontramos:
Podemos igualar os dois resultados e teremos o seguinte:
Vou separar em duas frações o lado direito para você visualizar melhor:
Um coeficiente já podemos determinar: o ! É o único expoente, então
Beleza?

E igualando os termos sem :
Podemos somar essas duas expressões e eliminar o termo :
E usar esse resultado para encontrar . Vou escolher a segunda equação:
Daí o valor de é:

Assim os valores dos coeficientes que satisfazem a integral são
E é isso!
Espero ter ajudado! Vamos para a próxima?