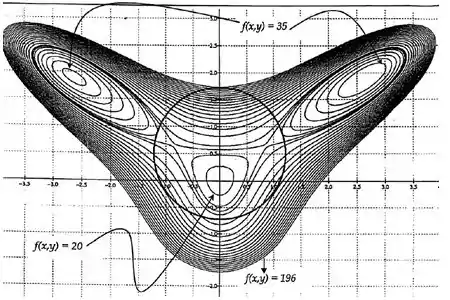
Considere a figura abaixo que representa as curvas de nível de uma função com derivadas parciais contínuas e uma restrição . (Circunferência)
a) Marque na figura todos os pontos críticos de .
b) Tendo por base o valor das curvas de nível indicado na figura classifique os pontos críticos em a)
c) Desenhe na figura o vetor gradiente da função no ponto
d) Indique, com um X sobre a figura, os pontos que são solução do seguinte sistema:
e) Olhando para a figura, você consegue concluir onde ocorrem os valores máximo e mínimo da função restrita à circunferência?
Passo 1
a) Cara, a gente tem as curvas de nível do gráfico de uma função. A ideia é aqui é usar nossa imaginação para ver como esse gráfico está em 3D, tá?
A gente precisa identificar os pontos críticos. São pontos onde as derivadas parciais zeram. Se zeram, a gente pode pensar que são pontos onde a taxa de variação (a derivada) muda de sinal.
Mas como a gente precisa que as derivadas zerem ao mesmo tempo, a gente vai ver se essa mudança de sinal ocorre ao mesmo tempo em duas direções perpendiculares. Aí a gente sabe que as duas derivadas parciais zeram, beleza?
Passo 2
Por exemplo, nesse ponto:

Na direção vermelha, nossa função cresce e depois decresce. E na direção azul, ele decresce e depois volta a crescer de novo. Aí mudamos de sinal em duas direções perpendiculares, então temos um ponto crítico.
Aí marcando todos os pontos onde acontece algo assim, teremos isso:
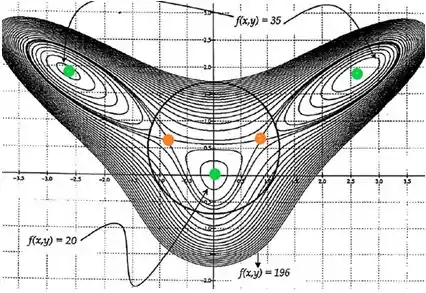
Passo 3
b) Cara, na curva de fora a gente tem um valor alto , e nas curvas interiores, a gente tem valores baixos, e . Isso mostra que o gráfico da nossa função é máximo nas bordas e tem seus mínimos no interior.
Percebe que os pontos verdes são os pontos mais baixos do nosso gráfico (tem os menores valores). Como a gente viu que eles são pontos críticos, podemos dizer que eles são pontos de mínimo. Em volta deles, a função parece um paraboloide elíptico virado para cima.
Saindo deles, a gente só consegue subir.
Mas nos pontos laranjas

Se a gente andar no sentido da setinha roxa, a gente sobe (aumenta ), mas se andar no sentido da setinha rosa, a gente desce (diminui ). Isso significa que a gente tem algo assim ao redor desses pontos:
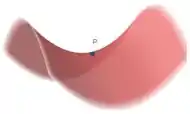
Por isso, esses são pontos de sela (se parecem até com uma sela de cavalo, né?),
Passo 4
c) Cara, esse é o ponto
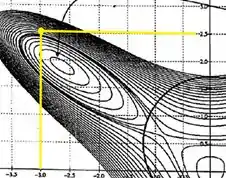
Para desenhar o vetor gradiente nele, a gente precisa lembrar que o vetor gradiente está sempre no sentido em que a função cresce mais, e ele é perpendicular a curva de nível que passa pelo ponto.
Se a gente desenhar um vetor normal a curva de nível que passa pelo nosso ponto, saindo do nosso ponto, temos algo assim:
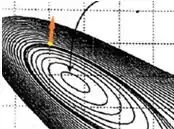
Percebe que ele aponta para o sentido onde a função cresce.
Passo 5
d) Vamos entender quem são os pontos que satisfazem esse sistema:
Dizer que
Significa que precisam pertencer a circunferência.
Passo 6
Agora o que quer dizer:
Cara, é o vetor gradiente da nossa função. Já é o vetor gradiente de , quando a gente escreve que a equação da circunferência é
Estamos querendo dizer que a circunferência é uma curva de nível de . E se ela é uma curva de nível de o vetor gradiente é normal a essa curva no ponto !
é uma constante. Então o que aquela equação está querendo dizer é que que a satisfazem, são pontos onde esses vetores gradientes são múltiplos um do outro. Ou seja, são paralelos!
Passo 7
Se os vetores normais a essas duas curvas forem paralelos em um ponto, os vetores tangentes também serão paralelos nesse mesmo ponto, certo?
O que isso quer nos dizer? Cara, esse sistema tem como resposta os pontos , que estão dentro da circunferência, e são pontos onde os vetores tangentes às duas curvas são paralelos entre si.
Aí marcando os pontos que têm essas características:
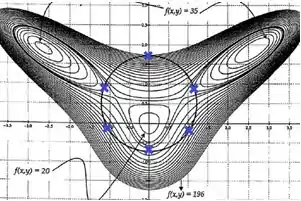
Passo 8
e) Cara, o ponto de máximo vai ser o ponto mais perto do ponto de máximo da função em si, que ocorre dentro da curva de .
Já o ponto de máximo está mais próximo da borda, que a parte mais alta do nosso gráfico. Percebe que a gente tem um ponto em cima da borda. Esse vai ser o ponto de máximo. Aí marcando esses pontinhos:
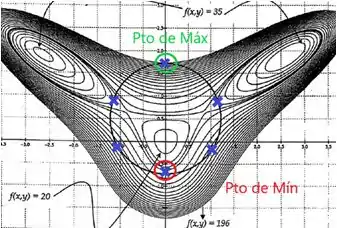
Resposta
Resposta nas imagens nos passos