UNICAMP – Cálculo 2 – Provas antigas – P2 – 2022.1 – 2
Determine e classifique os pontos críticos da função .
Passo 1
Fala, meus lindos e lindas 😊, tudo certinho com vocês? Bora pra questão sem pena. Primeira coisinha é a gente olhar isso de forma gráfica. Vai facilitar pro nosso entendimento mais a frente, confia em mim
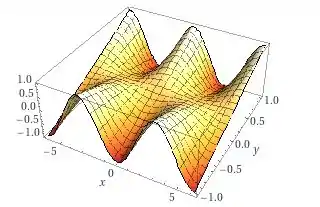
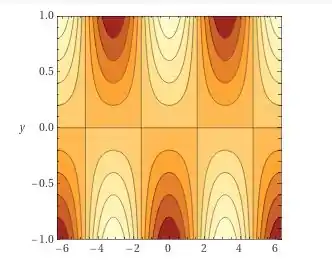
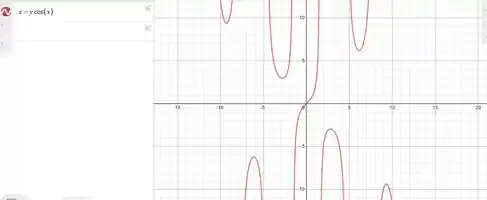
Agora bora lá determinar esses pontos críticos 😊
Passo 2
O que que a gente precisa pra determinar os pontos críticos? Isso mesmo, buscaremos os pontos que satisfazem a solução de Lagrange no formato:
Equivalentemente:
Aí vem o pulo do gato: Como o seno e cosseno nunca são simultaneamente nulos, então deve alguma hora ocorrer de ao mesmo tempo,
A segunda igualdade está no ponto de . Obtemos então infinitos pontos críticos
Passo 3
Para conseguirmos classificar esses pontos críticos, precisamos usar uma ferramenta que é a Hessiana. Nela, encontraremos um determinante de uma matriz feita a partir do Lagrangeano. O valor desse determinante vai nos definir se é um ponto de sela (ponto de virada crítica em e ). A Hessiana tem o formato:
Que pra nossa questão vai ficar:
Para , basta aplicamos os valores de e dentro da Hessiana. Esses valores são aqueles que encontramos no passo 2 ()
Logo,
Aplicando:
Temos então que:
Nosso determinante então é . Passa o Hessiano, quando temos:
Então aquele ponto é um ponto de sela. Como nosso determinante é , então é um ponto de sela. E é isso turminha! Finalizamos por aqui 😊. Se ainda restou alguma dúvida, ou gostaria de relatar alguma coisa, manda um feedback pra gente! Vamos adorar te responder, vai se rapidinho
Resposta
Pontos de sela.