UNICAMP – Cálculo 2 – Provas antigas – P2 – 2022.1 – 1a
1. (a) Utilize o método dos multiplicadores de Lagrange para encontrar as retas paralelas a reta e que sejam tangentes à elipse . Encontre os pontos de tangência.
Passo 1
Fala, meus lindos e lindas 😊, tudo certinho com vocês? Bora pra questão sem pena. Primeiro, utilizaremos o método de multiplicadores de Lagrange essas retas com as regras que a questão entrega pra gente. Você sabe como funciona ele? Vamo lá que eu te ensino. Primeiro, vamos desenhar essas duas formas pra gente se localizar melhor:
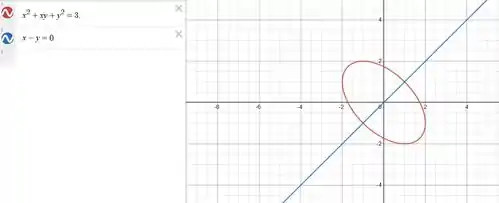
Assim, vamos encontrar as retas pararelas à reta azul e tangente na elipse, logo a forma dela deve ser igual a:
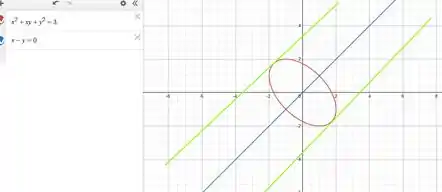
Passo 2
Como vamos usar o método de multiplicadores de Lagrange, vamos atrás da coisa mais importante nesse método, lembra qual é? É a constante . Essa constante existe tal que:
E no caso da elipse, o consiste em:
Pro nosso caso de (constante do lado direito da igualdade), temos então que:
O próximo passo é a gente montar o sistema para :
Para
Logo:
Isolando na primeira e segunda equações, e igualando, obtemos:
Isso significa que:
O que nos leva a:
Substituindo na última:
Passo 3
Mas o que a gente faz com isso? Ora, isso significa pra gente que se:
Então:
E, portanto, obtemos aqui 2 pontos no formato ):
Portanto, as retas são a curva de nível que passa por P1 e a curva de nível que passa por P2. Dessa forma, as retas que passam pelos 2 pontos, respectivamente:
Aplicando:
Logo:
Analogamente:
Plotando essas retas na nossa figura:
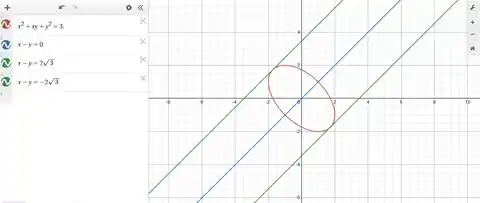
E é isso turminha! Finalizamos por aqui 😊. Se ainda restou alguma dúvida, ou gostaria de relatar alguma coisa, manda um feedback pra gente! Vamos adorar te responder, vai se rapidinho