Determine, se existirem, os pontos de máximo e mínimo absolutos de no domínio .
Passo 1
Primeiramente, a gente pode notar que a função é contínua (é um polinômio) e o domínio é fechado (é uma esfera), então o problema tem solução! Acho que você não perderia ponto na prova por não falar isso, mas também não custa nada! :)
Vamos começar achando os pontos críticos da .
Calculando as derivadas parciais:
Agora temos que igualar essas derivadas a zero:
Assim obtemos o único ponto crítico . Repare que
Então é o nosso primeiro candidato a ponto de máximo ou mínimo de em .
Passo 2
Agora temos que analisar a fronteira do conjunto , a esfera de equação
Vamos seguir nosso procedimento clássico:
- jogar tudo pra esquerda deixando zero na direita:
- chamar o lado esquerdo de :
- calcular gradiente da :
- usar o método dos multiplicadores de Lagrange:
- adicionar equação da fronteira de :
- obter o sistema
Passo 3
Show, vamos resolver esse sistema!
Pela equação temos
e pela equação :
Repare que não podemos ter e senão as equações estariam em contradição! Pela teríamos e pela . Então vamos ter 3 possibilidades:
- e
- e
Vamos olhar caso por caso!
Passo 4
Se , a equação fica:
Vamos testar se esses valores condizem com a equação :
Caso :
E caso :
Tudo certo! :)
Assim, obtemos 2 pontos candidatos: os pontos e .
Passo 5
Se e :
Pela equação temos .
Então a equação fica:
Substituindo na :
Mais 2 candidatos! Os pontos e .
Passo 6
Agora é a última possibilidade! Se e :
pela equação temos , o que na dá:
Agora vamos achar o com a equação :
Logo, os nossos último 2 candidatos são os pontos e . Até que enfim!
Passo 7
Recapitulando, os candidatos a ponto de máximo ou mínimo de no conjunto são:
Passo 8
Vamos calcular o valor da função em cada ponto para assim determinar qual é o máximo e qual o mínimo, show?
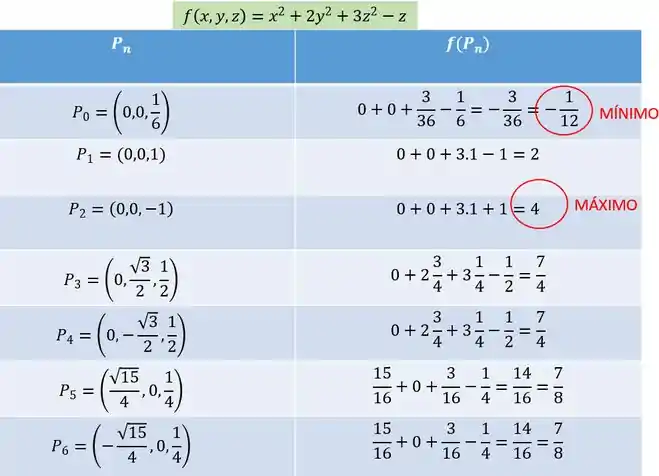
Portanto, o ponto de mínimo de em é e o ponto de máximo é , com valores mínimo e máximo respectivos de e .
Resposta
Ponto de mínimo: , valor mínimo .
Ponto de máximo: , valor máximo .