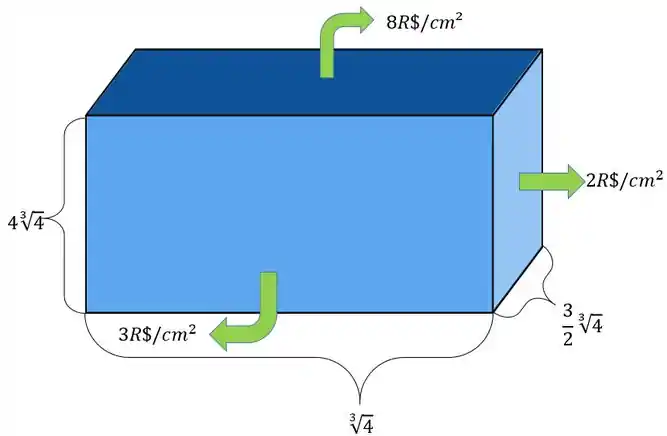
Deseja-se construir uma caixa retangular de de volume. O custo do material a ser utilizado é de por para a tampa e para o fundo, por para um par de lados opostos e por para o outro par de lados opostos. Determine as dimensões da caixa que minimizem o custo.
Passo 1
Temos que modelar o problema numa linguagem matemática.
Digamos que as dimensões da caixa são e . Então o volume da caixa é .
Vamos fazer um desenho dessa caixa pra gente visualizar melhor, show?
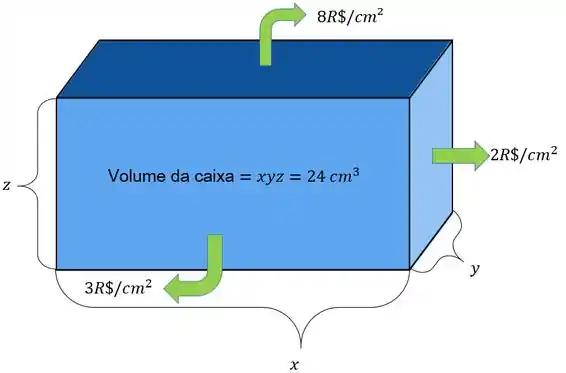
Beleza, vamos continuar! :)
Passo 2
Agora vamos analisar o custo de construção da caixa.
Ele depende das dimensões e da caixa, então vamos chamá-lo de .
Esse custo total é a soma dos custos de cada lado da caixa, né? E cada par de lados tem seu preço de construção, e suas dimensões. Então vamos achar o custo de cada par de lados!
Tendo a figura aí de cima em mente, dá uma olhada nessa tabela:
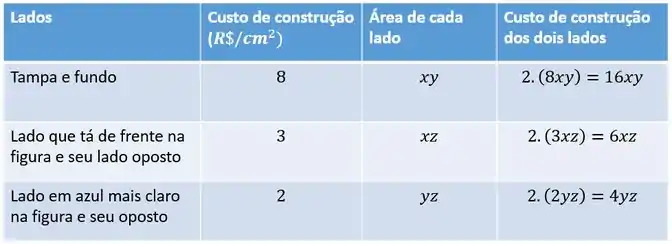
Excelente! Então o custo total é a soma do custo de construção dos 6 lados:
Passo 3
Recapitulando, queremos o mínimo de com a restrição . Isso não só tá pedindo, como tá implorando pra gente usar Lagrange! :D
Vamos criar a função assim temos
Então agora é só calcular os gradientes de e , o que vai ser tranquilo pra craques de derivação parcial como nós:
e
Passo 4
Show! Pelo método dos multiplicadores de Lagrange, temos
Acrescentando a condição , obtemos o sistema
Multiplicando a 1ª equação por , a 2ª por e a 3ª por , obtemos:
Logo:
Passo 5
Vamos separar essa equação em duas:
Não podemos ter dimensões negativas e o volume não é nulo então , e . Considerando isso, pelas equação temos:
E a equação nos dá:
Passo 6
Ótimo! Então usando a restrição obtemos
Então para e temos:
Só achamos uma solução: . Então esse é o ponto que minimiza o custo de construção da caixa.
Resposta