Qual o ponto da parábola que se encontra mais próximo do ponto ?
Passo 1
Ponto mais próximo? Hmm... me soa que temos uma “função distância”, e que queremos minimizá-la, certo? Mas, além disso, temos algo que serve como “guia”, como restrição para a função distância: a equação da parábola!
Como estamos trabalhando no , a distância entre dois pontos é dada por:
Neste caso, como queremos a distância em relação à ,
E aqui vem um pulo do gato que você vai querer guardar: Tá, queremos o mínimo da distância. Mas concorda que o mínimo dessa função coincide com o mínimo do seu quadrado? Isso acontece porque a distância é sempre um número positivo, e o mínimo de vai gerar o mínimo de ! A vantagem de pensar assim é que na hora de derivar, não teremos essa raiz em volta de tudo! Assim, vamos minimizar a função que batizaremos de , que é obtida elevando-se ao quadrado:
Passo 2
Show, agora que temos a função e a restrição, apliquemos LaGrange:
Em que é a equação da parábola, show? Os vetores gradiente são conseguidos derivando a função em relação a cada uma de suas variáveis:
Então pegamos e derivamos em relação a e a :
Agora, fazendo o mesmo para a parábola:
Passo 3
Agora voltamos à equação de LaGrange:
E podemos montar um sisteminha com as coordenadas acima igualadas e a função de restrição:
Da primeira equação, temos que , logo de cara! Colocando esse valor na equação de baixo temos:
E colocando esse valor na terceira equação, teremos:
Passo 4
É isso! Como não temos mais o que fazer, pois já descobrimos as coordenadas dos pontos, , aqui vai uma plotagem de quebra pra você visualizar melhor :)
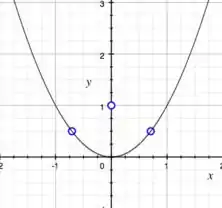
Resposta
Os pontos mais próximos de são