Determine o retângulo de perímetro máximo (com lados paralelos aos eixos coordenados) que pode ser inscrito na elipse de equação
Passo 1
Queremos maximizar a função perímetro do retângulo restrito a equação da elipse
Então, tá na cara que vamos usar o método de Lagrange.
A questão é que antes de sair correndo pra usar, vamos precisar pensar rapidinho quem é a nossa função , ou seja, aquela que a gente quer maximizar, ou seja, a função perímetro do retângulo.
Passo 2
Sabemos que nosso retângulo tem seus lados paralelos aos eixos coordenados.
Então se colocarmos o centro dele na origem, teremos algo mais ou menos assim:
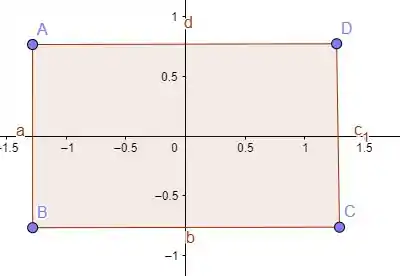
Se dissermos que o ponto tem coordenadas , então podemos dizer que o perímetro do nosso retângulo é
E o gradiente de é:
Passo 3
Agora sim! Nosso retângulo está restrito à elipse, assim,
E o gradiente de é:
Passo 4
Aplicando o método dos multiplicadores de Lagrange:
Igualando as coordenadas e adicionando a equação da restrição, ficamos com o sistema:
Passo 5
Vamos resolver esse sistema!
Igualando as duas primeiras equações:
Substituindo isso na equação da restrição:
OBS: estamos falando de uma medida de comprimento, por isso que eu não coloquei , ta bem?
E, como
E temos o ponto
Passo 6
Agora, para saber o perímetro máximo, é só substituir o ponto na função
Portanto, o retângulo de perímetro máximo inscrível na elipse tem vértice superior direito no ponto
E perímetro máximo igual a .
Resposta
o retângulo de perímetro máximo inscrível na elipse tem vértice superior direito no ponto
E perímetro máximo igual a .