Seja .
a) Exiba a matriz hessiana de no ponto e a aproximação quadrática de neste ponto.
b) Encontre um aberto tal que a matriz hessiana de em todo ponto seja estritamente positiva definida. Desenhe o aberto e, ao lado, sua fronteira.
c) Encontre um aberto tal que a matriz hessiana de em todo ponto seja indefinida.
d) Classifique os pontos críticos de .
e) Calcule o valor de máximo de restrita à curva
Dica: Considere que
Passo 1
a) Nossa função é
Para encontrar a sua hessiana, basta encontrar as segundas derivadas no ponto pedido e colocar na matriz!
Derivando em relação a , temos:
Derivando novamente em relação a teremos:
Show? Agora, façamos o mesmo para as derivadas em relação a :D
Derivando em relação a novamente,
Beleza? Agora basta encontrarmos as derivadas mistas! Pegando a derivada e derivando em relação a , teremos:
Passo 2
Agora podemos montar a matriz!
Ela é
Colocando as derivadas, fica:
Colocando no ponto ,
Passo 3
A aproximação quadrática no ponto vai ser
Temos quase tudo da fórmula, menos e
Já achamos as derivadas para o gradiente, elas são
Então
Isso nos diz que
Passo 4
b) Uma hessiana é estritamente positiva definida se, e somente se:
- Seu determinante é positivo
- é positiva
Vamos dar uma olhada no determinante?
Como ele deve ser maior que , temos:
Show? E para o segundo ponto, temos:
Passo 5
Agora, vamos resolver o sistema com essas duas inequações:
Vejamos... a primeira tem o termo , que nunca é negativo, certo? Logo, já que esse termo não vai mudar o sinal da expressão, podemos dizer que:
Show? Acabamos de ver que deve ser menor que !
Passo 6
Vamos olhar para a segunda inequação agora? Ela é:
Podemos colocar o em evidência, o que fornece:
Novamente, o termo não muda em nada o sinal da inequação, pois é sempre positivo e está multiplicando o termo entre parêntesis ;) Podemos dizer, então, que:
Passando o para o lado direito, temos:
E perceba que essa inequação é compatível com o que havíamos encontrado! Ela ainda fornece a relação entre e que faz com que a hessiana seja estritamente positiva definida!
Podemos dizer que o aberto , então, é:
Passo 7
Vamos ver, agora, que região é essa que encontramos? O que acha de começarmos pelo seu contorno, ou seja, colocando um sinal de igual na inequação? Fica:
Podemos escrever essa equação como:
Já deu pra ver que essa é uma curva exponencial... Vemos, também, que a medida que cresce, os valores de tendem a , e, quando , . E, ainda, a medida que tente ao infinito negativo, o termo tende ao infinito positivo, que, com o sinal de na frente, vai para o infinito negativo também!
Juntando essas informações, temos que a curva se parece com:
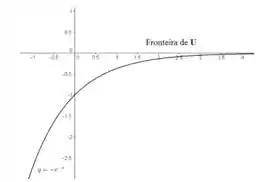
Como a inequação era , então estamos na região “menor que” a curva, ou seja, em baixo dela!
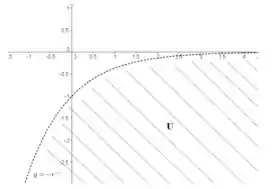
Passo 8
c) Para a hessiana ser estritamente indefinida, seu determinante deve ser menor que , ou seja,
Pelo mesmo mecanismo que do passo anterior, podemos colocar em evidência, que dá:
Como o termo não interfere em nada no sinal, temos:
Passando o para o lado direito, teremos:
E aí está a região definida pelo nosso aberto ! Ele pode ser escrito formalmente como:
Passo 9
d) Vamo que vamo! Agora é classificar pontos críticos... Do passo , temos que as derivadas parciais são:
Logo, os pontos críticos são aqueles que resolvem o sistema:
Pela primeira equação já vemos que, como o não se anula, então precisamos de .
Olhando agora, para a segunda, colocando o , teremos:
Para que isso ocorra, então , também! Assim, o único ponto crítico é , show?
Passo 10
Agora que temos o ponto, podemos jogar na expressão do determinante, que é:
Colocando , nela, teremos:
Como , então temos que é um ponto de sela! Ponto encontrado e classificado, letra detonada!
Passo 11
e) Vamos lá, última letra, aguente firme! Essa aqui é uma clássica de LaGrange, pois temos que encontrar o máximo/mínimo de uma função restrita a uma curva dada! Neste caso, a equação da nossa curva é:
A variação em entre e não importa agora pois só restringe o pedaço da curva que estamos tratando. Vamos encontrar os pontos e ver quais estão dentro dessa restrição de ;)
Sem mais enrolação, vamos montar o sistema com a equação do multiplicador e da restrição?
Passo 12
Agora, precisamos, para resolver esse sistema, encontrar os vetores gradientes de e .
O de já sabemos, é só juntas as primeiras derivadas no vetor:
Agora, para descobrir o vetor gradiente de , precisamos derivar a função. Temos:
E, assim, o vetor fica:
Passo 13
Agora que temos os vetores, podemos voltar no sistema:
E, igualando as coordenadas, fica:
Como as duas primeiras equações estão igualadas ao , podemos dizer que:
Passando o para o lado esquerdo, teremos:
Colocando o em evidência, fica:
E, dessa equação, vemos que, ou , para que seja , ou , para que se anulem os dois lados :D
Ok, temos as duas possíveis soluções do sistema...
Passo 14
Vamos verificar se elas são verdadeiras? Se colocarmos na equação da restrição, teremos:
Opa! não é uma opção de resposta! Lembra que está entre e , pela definição da nossa curva? Daí já vemos que não satisfaz nosso problema!
Passo 15
Vamos ver agora o que eu acontece colocando na restrição?
Show! Acabamos de encontrar o ponto como solução para o sistema! Vamos ver quando vale a função neste ponto?
E agora, como fazer para saber se é máximo ou mínimo?
Passo 16
A nossa curva é limitada! Isso significa que não basta ver os pontos críticos sobre ela, apenas, como acabamos de fazer! Temos que verificar o valor da função também para os seus pontos máximos e mínimos!
Eles ocorrem quando e quando , ou seja, nos limites definidos para pelo enunciado ;)
Quando , temos o igual a:
E o ponto a ser avaliado é . Seu valor em é:
E, como o enunciado disse, , logo, até é ponto de máximo!
Passo 17
Quando na curva, temos:
E o ponto a ser avaliado é . Colocando-o em , teremos:
Logo, é realmente o ponto de máximo e vale !
Resposta
a)
b)
Região: 
c)
d) O único ponto crítico é um ponto de sela, .
e) O valor máximo ocorre em