Deseja-se encontrar os pontos de máximo e mínimo de sobre o conjunto .
- O problema tem solução? Justifique.
- Em caso afirmativo, determine tais pontos.
- A função acima tem ponto de máximo sobre o conjunto ? E de mínimo? Justifique suas respostas.
Passo 1
a)
Essa é clássica!
Basta dizer que é um conjunto compacto (ele é limitado e fechado), e que é contínua em (é o produto de funções contínuas), então, pelo teorema de Weierstrass, o problema tem solução.
Passo 2
b)
Identificamos um problema de máximo e mínimo globais num conjunto fechado.
A primeira coisa a ser feita é procurar pelos pontos críticos da função. Então partiu!
Começando pelo gradiente da função:
Passo 3
Igualamos as derivadas parciais a zero:
Opa! Deu pra ver que deu ruim?
Pela 1ª equação, temos , mas substituindo isso na 2ª equação temos uma divisão por zero!
Portanto, não tem pontos críticos.
Passo 4
Antes de mais nada, uma boa vai ser a gente esboçar o conjunto pra entender melhor o que estamos fazendo:
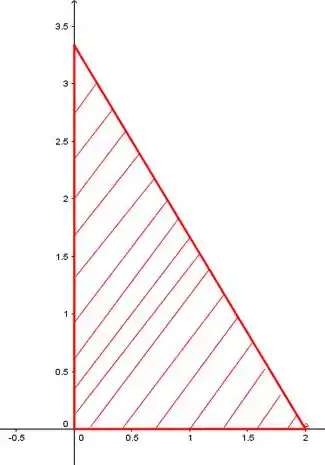
Passo 5
Ok, vamos continuar.
O próximo passo é separar os vértices da região, no caso, do triângulo.
Podemos ver tranquilamente que um dos vértices é a origem. Os outros dois são as interseções da reta 5 com os eixos coordenados.
No de cima temos , logo
No de baixo, :
Então vamos guardar os vértices e .
Esses são os nossos primeiros candidatos a ponto de máximo e mínimo globais de sobre o conjunto .
Passo 6
Agora vamos dar uma olhada nas fronteiras de , ou seja, os lados do triângulo.
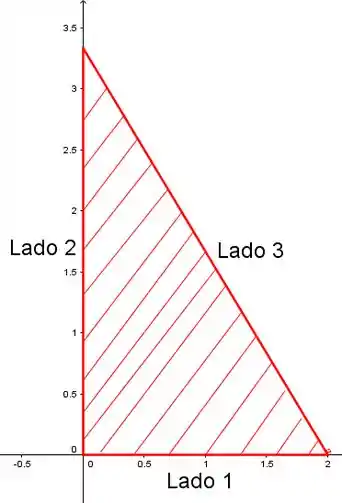
Vou defini-los assim:
Lado 1:
Lado 2:
Lado 3: , com
Passo 7
Começando pelo lado 1:
Portanto, em todo o lado 1 a função vale zero. Vamos guardar esse resultado pra depois.
Passo 8
Agora vamos pro lado 2:
Da mesma forma, temos
Assim como no lado 1, no lado 2 todo a função vale zero. Guardamos esse resultado também.
Passo 9
No lado 3 temos
Então passa a depender só de :
Vish, que função feia... Teríamos que calcular essa derivada e ver onde ela se anula, o que daria um trabalho do cão.
Sabe o que vamos fazer pra evitar isso?? Continua no próximo passo...
Passo 10
Multiplicadores de Lagrange!!
Espero que a sua curiosidade tenha aguentado esse aproximadamente 1 segundo de suspense. Enfim, é isso, quando a coisa aperta chamamos o parça Lagrange que ele nunca falha.
Temos que achar os máximos/mínimos da função sob a reta .
Pegamos a equação da reta e jogamos tudo pra esquerda:
Chamamos o lado esquerdo de :
Assim, a equação da reta é .
Calculamos o gradiente da :
Aplicamos os multiplicadores de Lagrange:
Passo 11
Calculamos as derivadas parciais da láá atrás, lembra? Então o determinante é:
Vamos deixar tudo com na esquerda e tudo com na direita:
Passo 12
Agora usamos a equação da restrição:
Como , obtemos
Ótimo, então no lado 3 temos um ponto candidato: o ponto .
Passo 13
Recapitulando, temos os pontos
além dos lados 1 e 2, onde vale zero.
Agora só nos resta calcular o valor de nesses 4 pontos. Temos
Hmm, isso é meio chato de calcular, e na verdade nem precisa. Ele não pediu os valores máximo e mínimo, e sim os pontos. E podemos ver que
Como todos os outros valem zero, o ponto é o ponto de máximo global de sobre .
E os pontos de mínimo são todos os pontos que estão sobre os 2 segmentos
Passo 14
c)
Esse novo conjunto é que nem o conjunto , mas sem os 2 segmentos onde a função vale zero, que são os lados 1 e 2, mais os vértices do triângulo.
Mas essa alteração não afetou nosso ponto , ele continua ali de boa, então ele é o ponto de máximo global de sobre esse novo conjunto.
Passo 15
O problema mesmo é pra tratar do mínimo. Vamos com calma... a função é
Isso com e . Você concorda comigo que ?
E temos
Podemos nos aproximar o quanto quisermos de zero sem nunca alcançá-lo, então não existe ponto de mínimo.
Resposta
a) Sim, pelo teorema de Weierstrass.
b)
Ponto de máximo:
Pontos de mínimo:
c)
Ponto de máximo:
não assume ponto de mínimo nesse conjunto.