Considere a superfície quádrica dada pela equação
(a) Identifique e esboce o gráfico de mostrando as curvas de interseção com os planos coordenados, , e .
(b) Determine as equações paramétricas da curva , interseção de com o plano .
(c) Determine as equações paramétricas dos planos tangentes à que são paralelos ao plano .
Passo 1
(a)
Queremos identificar a superfície, então vamos ver se reconhecemos a sua equação. Tá parecendo com as quádricas que a gente conhece da forma
Então vamos ajeitar a equação da pra ficar algo assim, beleza? Temos
Mas queremos 1 do lado direito, então vamos dividir tudo por 36:
Show! E como os 3 sinais são positivos, essa é a equação de um elipsoide!
Inclusive podemos notar que ele é centrado na origem: não tem nenhum termo , ou , apenas e .
Passo 2
Vamos ver o que acontece com a quando ela intercepta os planos coordenados.
- No plano :
- No plano :
- E no plano :
- No plano :
- No plano :
- No plano :
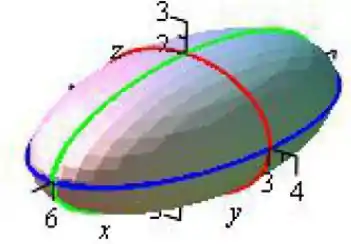
- a elipse do plano de vermelho
- a elipse do plano de verde
- a elipse do plano de azul
E todas essas são equações de elipses, o que não é muito surpreendente, já que é um elipsoide!
Passo 3
Agora vamos dar uma olhada em cada uma dessas elipses pra ajudar a gente a esboçar. A equação de uma elipse é da forma
onde é a metade do eixo maior e é a metade do eixo menor. Isso vai ajudar a gente a determinar se as elipses são mais “gordas”, esticadas, etc.
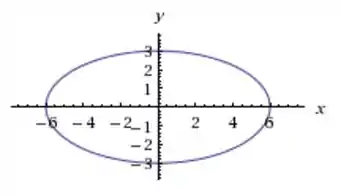
Temos e , então ela é um pouco mais comprida no sentido do eixo :
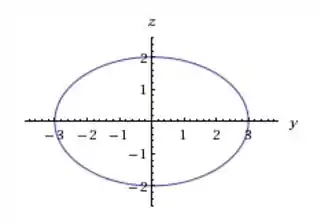
Essa tem e , ou seja . Então ela vai ser mais esticada:
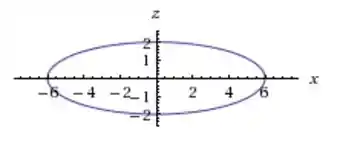
Essa tem então vai ser meio que um intermediário das 2 outras:
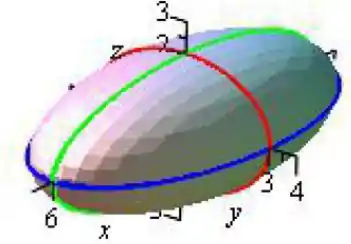
Ou seja, o elipsoide vai ser mais alongado no sentido do eixo !
Passo 4
Agora não tem jeito, vamos esboçar ! Temos que destacar as interseções com os planos coordenados, que são essas elipses aí de cima, então vamos fazer da seguinte forma:
Então o nosso elipsoide vai ser:
Passo 3
(b)
Agora queremos as equações paramétricas da curva , interseção de com o plano .
Já vimos que essa curva é a elipse de equação
Vamos lembrar como se parametriza uma elipse! Se temos
então uma parametrização é
Logo, uma parametrização de é:
Podemos verificar que
Passo 4
(c)
Agora queremos os planos tangentes a que sejam paralelos ao plano .
Mas se os planos são paralelos, então os vetores normais deles também são, certo?
E o vetor normal do plano a gente já sabe qual é! Lembrando que se temos um plano então o vetor é normal ao plano. Logo, o vetor é um vetor normal ao plano .
Então agora só precisamos dos vetores normais dos planos tangentes a ! Então agora se liga no passo a passo:
Passo 5
Vamos pegar a equação da , jogar tudo pro lado esquerdo, deixando zero na direita:
Passo 6
Vamos chamar o lado esquerdo da equação de :
Assim, a equação da fica
Passo 7
Vamos calcular o gradiente da :
Agora nós podemos constatar que o gradiente de em um ponto qualquer de é um vetor normal ao plano tangente a nesse ponto!
Passo 8
O que concluímos disso tudo?
Simples, que pro plano tangente a num ponto ser paralelo ao plano os vetores normais deles têm que ser paralelos, ou seja:
Obtivemos um sistema!
Logo:
Então os pontos de onde os planos tangentes são paralelos ao plano são da forma
Passo 9
Agora só falta achar esse ! E pra isso vamos usar o fato dos pontos pertencerem a e respeitarem sua equação:
Ufa! Afinal o deu esse valor estranho aí!
Passo 10
Enfim, os pontos que queríamos são da forma
Por causa desse “” são 2 pontos, digamos e :
e
Mas afinal, a gente quer a equação dos planos tangentes! Que são da forma
O vetor é paralelo ao vetor normal desses planos, então ele serve de vetor . Ou seja, as equações dos planos são:
e
Resposta
(a)
(b)
(c)
e
com e