USP – Cálculo 2 – P1 – 2022.2 – Questão 4.
4) Seja dado por . Decida se admite plano tangente ao seu gráfico no ponto e, em caso afirmativo, escreva a equação deste plano.
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, a questão pede pra gente verificar se a função admite plano tangente no ponto , e descobrir qual é a equação desse plano caso ela o admita. E pra fazer isso podemos usar os seguintes passos:
Caso seja necessário, substituir por na equação da superfície
Jogar todas as variáveis para o lado esquerdo da equação e achar
Chamar de a expressão deixada no lado esquerdo da equação
Calcular gradiente de :
Calcular gradiente de no ponto :
O vetor normal será
Encaixar a tudo na equação do plano
Passo 2
Vamos começar fazendo . E jogar todas as variáveis para o lado esquerdo:
Passo 3
Vamos encontrar logo qual é a coordenada do ponto dado no enunciado? É só a gente substituí-lo na expressão aqui de cima:
No ponto :
Passo 4
Ok, agora temos que
Passo 5
Estamos prontos para calcular o vetor gradiente! Lembra da expressão dele?
Como , vamos calcular as derivadas parciais
Passo 6
Assim, nosso vetor gradiente, no ponto dado, , fica:
Mas essa coordenada não está definida. Assim, como a coordenada . Veja
Apenas
Isso nos mostra que não é possível determinar o plano tangente ao gráfico da função dada.
Também podemos ver isso analisando seu gráfico. Veja:
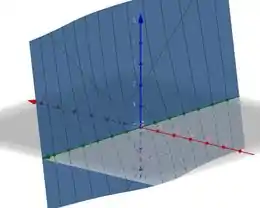
Então concluímos que não admite plano tangente ao seu gráfico no ponto
Prontinho!!
Resposta
Resposta:
não admite plano tangente ao seu gráfico no ponto .