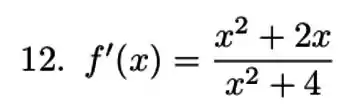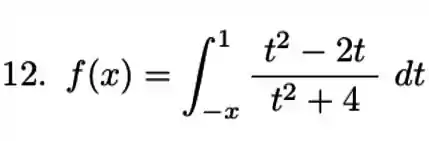
Passo 1
Aqui vamos ter que usar o Teorema Fundamental do Cálculo para encontrar . Só que aqui o limite superior é a constante então vamos ter que utilizar aquela propriedade para inverter os limites.
Passo 2
Agora nosso limite superior é
Para encontrar a derivada temos que usar a regra da cadeia. Primeiro substituímos a variável por . Depois, multiplicamos pela derivada de .
Prontinho.
Resposta
Exercícios de Livros Relacionados
Use a parte 1 do teorema fundamental do cálculo para encontrar a derivada da função: h x = ∫ 2 1 / x arctan t d t
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela. ∫ cos x - 2 sen ( x ) d x
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x
A região no primeiro quadrante, limitada pela curva y = 5 - x x + 1 2 , pelo eixo x e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.
Em uma cidade com 12000 pessoas, a taxa de crescimento de uma epidemia de gripe é conjuntamente proporcional ao número de pessoas tiveram a gripe e ao número de pessoas que não a contraíram. Cinco dia