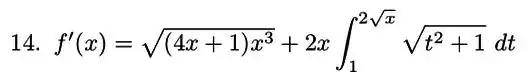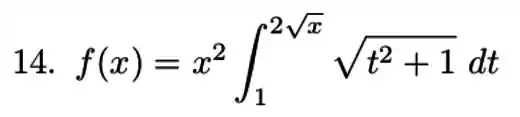
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema Fundamental do Cálculo

Ver Teoria
Exercício 130123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para encontrar f ' x primeiro devemos que aplicar a regra do produto, ou seja,

f ' ( x ) = d x 2 d x   ∫ 1 2 x t 2 + 1 + x 2 d d x ∫ 1 2 x t 2 + 1

f ' x = 2 x ∫ 1 2 x t 2 + 1 + x 2 d d x ∫ 1 2 x t 2 + 1

Passo 2

Agora, precisamos substituir 2 x e aplicar a regra da cadeia para calcular a derivada da integral da segunda parte da expressão

f ' x = 2 x ∫ 1 2 x t 2 + 1 + x 2 d d x ∫ 1 2 x t 2 + 1

x 2 d d x ∫ 1 2 x t 2 + 1 = x 2   2 x 2 + 1   .   2 x '

x 2 d d x ∫ 1 2 x t 2 + 1 = x 2   4 x + 1   .   2 1 2 x

Se simplificarmos um pouco

x 2 d d x ∫ 1 2 x t 2 + 1 = 4 x + 1 x 3

Passo 3

Por sim, falta apenas juntar as duas partes da expressão do primeiro passo

f ' x = 2 x ∫ 1 2 x t 2 + 1 + x 2 d d x ∫ 1 2 x t 2 + 1

f ' x =   2 x ∫ 1 2 x t 2 + 1 + 4 x + 1 x 3

Resposta

Exercícios de Livros Relacionados

Use a parte 1 do teorema fundamental do cálculo para encontrar a derivada da função: h x = ∫ 2 1 / x arctan ⁡ t d t
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela. ∫ cos ⁡ x - 2 sen ⁡ ( x ) d x
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x
A região no primeiro quadrante, limitada pela curva y = 5 - x x + 1 2 , pelo eixo x e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.
Em uma cidade com 12000 pessoas, a taxa de crescimento de uma epidemia de gripe é conjuntamente proporcional ao número de pessoas tiveram a gripe e ao número de pessoas que não a contraíram. Cinco dia