Cálculo de Volume através de Integrais
Seja
Mostre que é uma função par
Calcule
Calcule a primeira derivada da função ,
Calcule
Determine a equação da reta tangente ao gráfico de em
Determine os pontos críticos de , e classifique cada um deles.
Passo 1
Para mostrar que essa função é par, devemos garantir que:
Para isso, basta olhar para o único termo que varia para , o limite de integração inferior:
E veja, nele temos o elevado ao quadrado. A função é uma função par. Multiplicando ela por e subtraindo , teremos a mesma situação de paridade na função!
Logo, é função par pois é par.
Passo 2
Aplicando :
Os limites de integração são iguais. Logo, essa função será nula em , independente da função de a ser integrada.
Passo 3
Vamos derivar pelo Teorema Fundamental do Cálculo. Começamos abrindo a função em duas, uma de até uma constante qualquer. Outra de até . Com isso, aplicamos o teorema nas duas:
Aplicando o TFC:
Passo 4
Aplicando em :
Passo 5
Para achar a reta tangente a nesse ponto , precisamos da derivada, que será o coeficiente angular e do valor de para aplicar o ponto na equação da reta:
Temos que :
Além disso,
Assim, aplicando a reta em
Logo, a reta será:
Passo 6
Os pontos críticos de são aqueles em que:
Vale . Assim, reparando que o denominador é um termo elevado a expoente par somado a uma constante positiva, vemos que o denominador será sempre positivo.
Tudo fica na análise do numerador então:
Teremos três pontos críticos:
Passo 7
Classificando os pontos, devemos ver se são pontos de máximo ou de mínimo. Para isso, vamos fazer o quadro de sinais de :
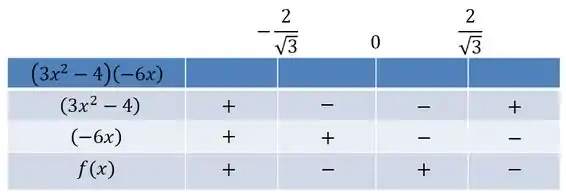
Como dá para ver, em temos a derivada positiva antes e negativa depois, o que gera um ponto de máximo. O mesmo acontece em .
Já em temos um ponto de mínimo, pois a derivada é negativa antes e positiva depois.