- Apresente:
- O teste da Derivada Primeira.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para gente apresentar o teste da derivada primeira. Então o lance aqui é a gente mostra que teste é esse e como ele funciona. Beleza?
Vem comigo que te ajudo com isso.
Passo 2
O teste da derivada primeira está associado à classificação de pontos críticos de uma função.
Os pontos críticos são aqueles pontos onde a função tem derivada igual a zero, e podemos classifica-los como pontos de máximo, de mínimo ou pontos de sela.
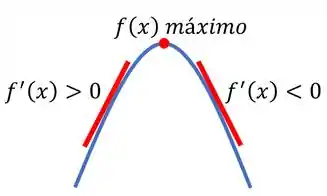
A ideia básica é a seguinte, para pontos de máximos da funç��o, a derivada de valores a esquerda desse ponto é positiva e a derivada de valores a direita é negativa. Pense nas derivadas como o coeficiente angular da reta tangente à curva: a esquerda do ponto a reta tangente é crescente, então a derivada é positiva, já a direita do ponto a reta tangente é decrescente, então a derivada é negativa.
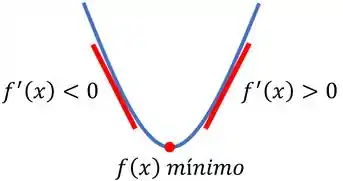
Para mínimos, podemos usar o mesmo raciocínio, e aí vamos ter o contrário: a derivada de valores a esquerda é negativa, já a derivada de valores a direita é positiva.
Assim, o teste da derivada primeira consiste em acharmos os pontos críticos fazendo , e depois analisarmos o sinal da derivada para pontos próximos aos pontos críticos.
E definimos dessa maneira:

Cuidado! ao escolher valores de referência à esquerda e à direita de um ponto crítico, tenha certeza de que eles não passem por nenhum outro ponto crítico 😉.
Resposta
No desenvolvimento.