Sejam uma constante positiva e satisfazendo:
E
- Determine os pontos críticos, intervalos em que é crescente e intervalos em que é decrescente.
- Determine e use o teste da derivada segunda para classificar os pontos críticos de
- Determine os intervalos em que a concavidade do gráfico de é para cima, os intervalos em que ela é para baixo e os pontos de inflexão do gráfico de .
- Usando os itens anteriores, faça um esboço do gráfico de supondo que
Passo 1
Bora enfrentar essa questão gigante, pessoal! O primeiro pedido é para a gente identificar os pontos críticos da função e quando isso acontece? Quando a derivada da função não existe ou a derivada é igual a zero:
O que já nos foi dado é que a derivada da função é:
Vamos começar pensando aqui: tem algum valor de que faz com que essa função não exista? Não, então só vamos poder encontrar o ponto crítico se igualarmos essa função a zero:
Como é uma constante positiva, ou seja, maior que zero e a função:
É sempre maior que zero, então a única parcela da derivada que pode tornar a derivada igual a zero é:
Então encontramos um único ponto crítico:
Passo 2
Como temos que analisar o crescimento e decrescimento, temos que dividir essa derivada da função nas parcelas dos produtos que são:
E
E vamos dividir a análise de sinal de até o nosso ponto crítico e depois até :
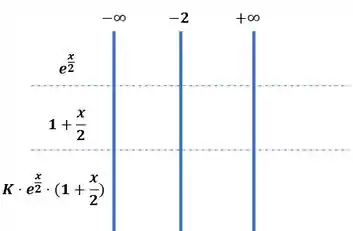
Vamos pensar: Se substituirmos o valor de por um valor negativo ou positivo em , sempre encontraremos um valor positivo:
Então nosso quadro fica dessa forma:
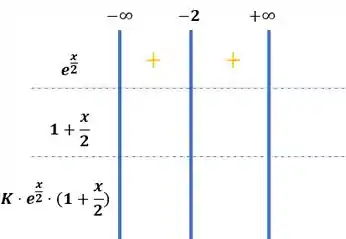
Agora se substituirmos o valor de por um valor entre e , nós vamos encontrar um valor negativo para:
Enquanto se substituirmos o valor de por valores maiores que , então encontramos valores positivos para a função:
Nosso quadro fica dessa forma:
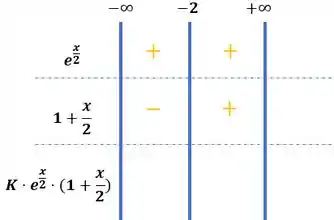
Vamos juntar isso tudo, como a constante é positiva, então o produto entre valores positivos e valores negativos é igual a valores negativos. Por outro lado, o produto entre valores positivos é igual a um resultado positivo. Nosso quadro então:
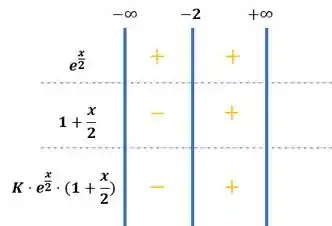
Agora temos que lembrar que a função é crescente quando a derivada é maior que zero, enquanto a função é decrescente quando a derivada é menor que zero:
Essa foi a letra “a”!
Passo 3
Para a letra “b”, temos que aplicar o teste da Segunda Derivada para classificar o Ponto Crítico. A primeira derivada foi dada:
Vamos derivar novamente para encontrar a Segunda Derivada:
Vamos aplicar a Regra do Produto:
Como sabemos que a derivada da exponencial e ela mesma vezes o expoente:
Enquanto a derivada da divisão entre e um número é:
Então nossa Segunda Derivada é:
Melhorando essa expressão, nós chegamos em:
Agora no teste da Segunda Derivada, vamos aplicar o valor do Ponto Mínimo na função que encontramos:
Ou seja, a Segunda Derivada assume um valor positivo! E o que significa quando a segunda derivada do ponto crítico dá um valor maior que zero? Encontramos um Ponto de Mínimo!
Resposta da letra “b” concluída com sucesso!
Passo 4
Para começar bem a letra “c”, vamos encontrar os pontos de inflexão! Esses pontos ocorrem onde a segunda derivada é igual a zero ou não existe:
Bom, nós já calculamos a segunda derivada no passo anterior:
Olhando para essa função, existe algum que faz com que a função não existe? Não, então não temos esse tipo de Ponto de Inflexão. Vamos verificar então quais são os valores de que fazem com que a segunda derivada seja igual a zero:
Bom, já sabemos e são sempre maiores que zero, então o único jeito que podemos tornar a segunda derivada igual a zero, é fazer:
Então:
Encontramos o ponto de inflexão igual a:
Passo 5
Mas para que serve o ponto de inflexão? É ele que determina a mudança da concavidade da função, ou seja, vamos montar aquele quadro que fizemos para analisar o sinal da função para valores antes e depois do ponto de inflexão:
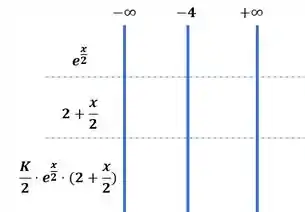
Como já falamos, para qualquer valor de , a função sempre será maior que zero:
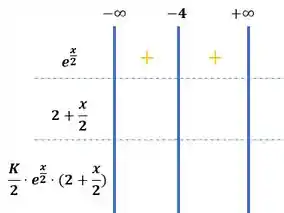
Enquanto para valores de menores que , a função terá valores negativos. Isso se inverte quando colocamos valores de maiores que , nossa função toma valores positivos:
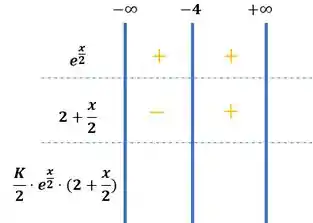
Agora se multiplicarmos essas partes, teremos que a Segunda derivada assume valores negativos, quando e valores positivos, quando >
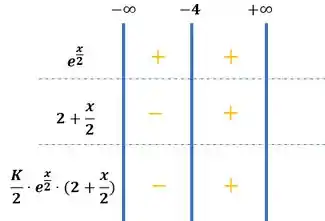
Logo, o estudo da concavidade aponta que como a derivada segunda é negativa no intervalo e é positiva no intervalo , então:
Passo 6
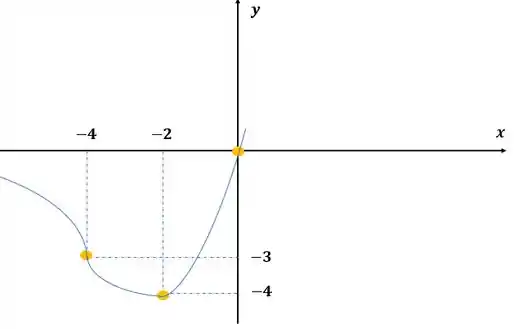
Para montarmos o gráfico, o enunciado nos deu os seguintes pontos:
Então vamos colocar esses pontos no gráfico:
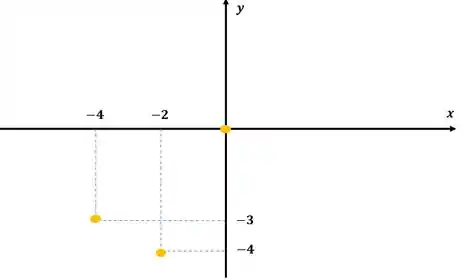
Colocando a concavidade para baixo para valores onde e concavidade para cima após , então temos:
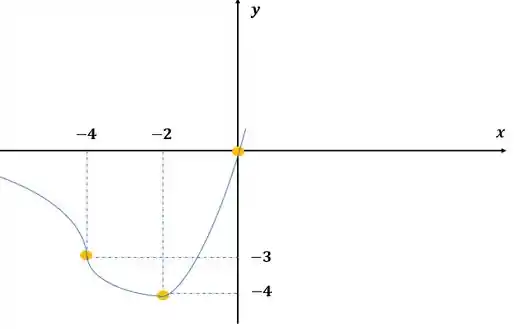
Resposta
- Ponto Mínimo