Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teste de Crescimento e Decrescimento

Ver Teoria
Exercício 412356789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Regras de Derivação I

Seja f x = x 2 e x - 1

( c ) Determine os intervalos do domínio de f onde a sua derivada seja positiva, negativa ou nula.

Passo 1

Para saber onde os intervalos da derivada vai ser positiva, negativa ou nula, temos que começar achando a derivada. Depois vamos fazer a análise de sinal dessa função.

Vamos usar a Regra do Produto para essa questão:

Temos o produto de x 2 com e x - 1

f ' x = x 2 ' e x - 1 + x 2 e x - 1 '

f ' x = 2 x e x - 1 + x 2 e x - 1 '

Opa, temos que fazer a derivada de uma função exponencial com uma função no expoente. Agora vamos precisar fazer a regra da cadeia em e x - 1

Passo 2

Vamos fazer a derivada de g x = e x - 1 , chamei de g x só para facilitar nossa conta.

Repara que temos duas funções ali, uma é a função que está no expoente

u x = x - 1

A outra é o e elevado a essa função, que no fundo é a função

h x = e x

Assim

g x = h u x

Aplicando a regra da cadeia, teremos

g ' x = h ' u x u ' x

Vamos achar a derivada de h e de u

h ' x = e x

u ' x = 1

Assim

g ' x = e u x . 1 = e x - 1

Passo 3

Agora, voltando para f x , tínhamos

f ' x = 2 x e x - 1 + x 2 e x - 1 '

Substituindo o valor que achamos de e x - 1 ' , vamos ter

f ' x = 2 x e x - 1 + x 2 e x - 1

Colocando e x - 1 em evidência, vamos ter

f ' x = ( 2 x + x 2 ) e x - 1

Passo 4

Vamos fazer o quadro de sinais de f ' ( x ) , lembrando que a exponencial é sempre positiva e por isso não importa no nosso sinal de f ' ( x ) :

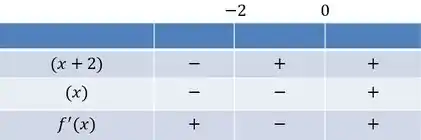
Dessa forma, a derivada de f é positiva no intervalo ] - ∞ , - 2   ∪   0 , + ∞ [ . Ela é negativa em ] - 2,0 [ e vale 0 quando x = 0 e quando x = - 2 .

Resposta

P o s i t i v a :   x   ∈   ] - ∞ , - 2   ∪   0 , + ∞ [

N e g a t i v a :   x   ∈   ] - 2,0 [

N u l a : x = 0 ; x = - 2

Exercícios de Livros Relacionados

Em uma investigação de assassinato, a temperatura do corpo era 32,5 ºC às 13h30 e 30,3 ºC uma hora depois. A temperatura normal do corpo é 37,0 ºC, e a temperatura do ambiente era 20 ºC. Quando o assa
Demonstre que quando x → ∞ , e x cresce mais rapidamente que x 2 para qualquer inteiro positivo, até mesmo x 1.000.000 . Dica: qual é enésima derivada de x n ?
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Mostre que 1 + x 31 + 1 3 x se x0 e confirme a d
53-54. Em cada parte, determine se a afirmação é verdadeira ou falsa. Se falsa, encontre funções para quais a afirmação não é válida.53. b) Se f e g forem crescentes em um intervalo, então f . g també
Nos Exercícios de 1 a 40, faça o seguinte: (a) ache os extremos relativos de f pelo teste da primeira derivada; (b) determine os valores de x nos quais os extremos relativos ocorrem; (c) determine os