USP– Cálculo 1 – Lista 2 – Questão 1.6a
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
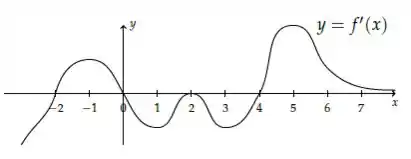
- Em que intervalos é crescente ou decrescente?
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá o gráfico da função derivada de uma função
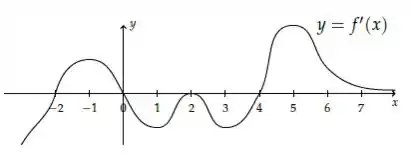
E faz uma pergunta
Em que intervalos é crescente ou decrescente?
E agora, como determinar isso?
Sabemos que uma função é crescente quando sua derivada é POSITIVA, enquanto é decrescente quando sua derivada é NEGATIVA
Sendo assim é só a gente olhar pro gráfico da derivada e ver onde ela é positiva e onde é negativa!
Beleza?
Bora lá!
Passo 2
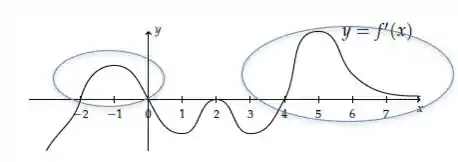Retomando o gráfico dado temos
A derivada é positiva (está acima do eixo horizontal) em:
E também
beleza? Nesses dois intervalos temos que a função é crescente!
Passo 3
Agora os intervalos onde ela é negativa são
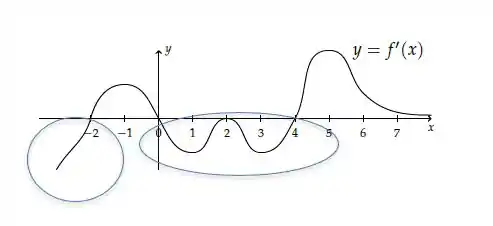e os intervalos
E também
E é isso! Até a próxima!
Resposta
Exercícios de Livros Relacionados
Em uma investigação de assassinato, a temperatura do corpo era 32,5 ºC às 13h30 e 30,3 ºC uma hora depois. A temperatura normal do corpo é 37,0 ºC, e a temperatura do ambiente era 20 ºC. Quando o assa
Demonstre que quando x → ∞ , e x cresce mais rapidamente que x 2 para qualquer inteiro positivo, até mesmo x 1.000.000 . Dica: qual é enésima derivada de x n ?
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Mostre que 1 + x 31 + 1 3 x se x0 e confirme a d
53-54. Em cada parte, determine se a afirmação é verdadeira ou falsa. Se falsa, encontre funções para quais a afirmação não é válida.53. b) Se f e g forem crescentes em um intervalo, então f . g també
Nos Exercícios de 1 a 40, faça o seguinte: (a) ache os extremos relativos de f pelo teste da primeira derivada; (b) determine os valores de x nos quais os extremos relativos ocorrem; (c) determine os