UFCG, Sem Campus, Cálculo Diferencial e Integral I, 3º Estágio - 2016.1, Questão 3a
Dada a função . Determine:
a) intervalos de crescimento e decrescimento e extremos locais.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente determinar os intervalos onde a função é crescente, decrescente e seus extremos locais (máximos e mínimos).
Como a derivada é uma taxa de variação, nós podemos usar ela pra verificar a função. Se a derivada, nossa função é crescente no intervalo, se for negativa, ela é decrescente.
Então, o que nós vamos fazer é calcular a derivada e fazer o estudo de sinal. Em seguida, vamos determinar os extremos locais fazendo .
Então, vamos lá!
Passo 2
Vamos calcular a derivada da função :
Podemos colocar em evidência:
Cada termo vai ser zero, quando ou quando , esses também são os pontos críticos da nossa função.
Agora vamos montar o quadro de sinais pra entender o comportamento dessa função:
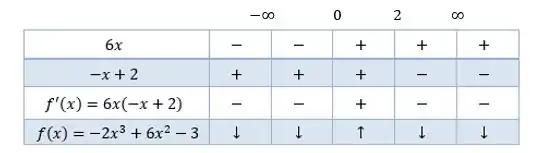
Na terceira linha, a gente faz a multiplicação dos sinais. Nos locais onde a derivada é positiva, a nossa função é crescente, como indica a setinha na quarta linha, e nos locais onde a derivada é negativa, a função a decrescente, como também indica a setinha.
Então, nosso intervalo de crescimento é:
E nossos intervalos de decrescimento são:
E nossos extremos locais são os pontos onde a derivada é zero, no caso, e . Repare que é um ponto de mínimo, e é um máximo local.
Prontinho, galera! Até a próxima! 😉