UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Raphael Constant - Lista 7 - Esboço de gráficos e Regra de L'Hôpital, Questão 1b
Determine o intervalo de crescimento e decrescimento da função
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de calc1. Nosso objetivo é descobrir qual é o intervalo de crescimento e decrescimento da função
Como fazemos isso? Precisamos ver o sinal da primeira derivada. Se o sinal é positivo a função é crescente naquela região, se for negativo é decrescente.
Passo 2
Derivando temos:
Logo
Vamos fazer o estudo de sinal. Primeiro achando as raízes dessa equação
ou
ou
Vamos fazer o estudo de sinal de cada uma das partes
e
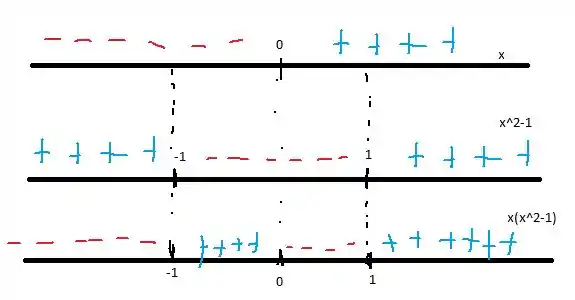
Logo,
se
Então
se
Então
Logo, a função é crescente em
E decrescente em
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Exercícios de Livros Relacionados
Em uma investigação de assassinato, a temperatura do corpo era 32,5 ºC às 13h30 e 30,3 ºC uma hora depois. A temperatura normal do corpo é 37,0 ºC, e a temperatura do ambiente era 20 ºC. Quando o assa
Demonstre que quando x → ∞ , e x cresce mais rapidamente que x 2 para qualquer inteiro positivo, até mesmo x 1.000.000 . Dica: qual é enésima derivada de x n ?
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Mostre que 1 + x 31 + 1 3 x se x0 e confirme a d
53-54. Em cada parte, determine se a afirmação é verdadeira ou falsa. Se falsa, encontre funções para quais a afirmação não é válida.53. b) Se f e g forem crescentes em um intervalo, então f . g també
Nos Exercícios de 1 a 40, faça o seguinte: (a) ache os extremos relativos de f pelo teste da primeira derivada; (b) determine os valores de x nos quais os extremos relativos ocorrem; (c) determine os