UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.3a
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
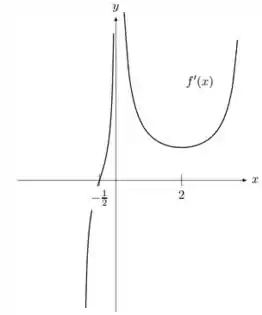
Responde o que se pede:
a) Os intervalos onde é crescente, e onde é decrescente.
Passo 1
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Com essas informações precisamos determinar os intervalos em que é crescente, e os intervalos em que é decrescente.
A ideia é olharmos para a derivada de , se:
Então, vamos usar o gráfico dado para obter essa informação.
Passo 2
Vamos analisar o gráfico de :
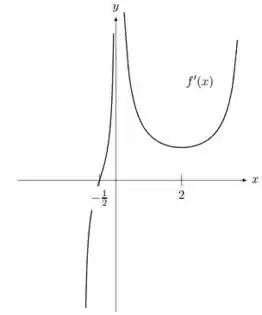
Os trechos em que ocorre , são:
Então, nesses intervalos temos crescente.
Os trechos em que ocorre são:
Então, nesse intervalo temos decrescente.
Prontinho galera, bem direto ao ponto essa primeira parte.
Vamos continuar estudando juntos os próximos itens 😉