Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teste de Crescimento e Decrescimento

Ver Teoria
Exercício 521234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFU, Sem Campus, Cálculo 1, Prof° Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 3.9b

Use um recurso gráfico para determinar os intervalos de crescimento e decrescimento das funções:

( b )   g ( x ) = 2 x 2 - 12 x + 20 x 2 - 6 x + 9 ,   x ∈ ℝ - { - 3 } .

Passo 1

Oiiie, tudo certinho contigo?

O enunciado nos dá a função

g ( x ) = 2 x 2 - 12 x + 20 x 2 - 6 x + 9

precisamos encontrar os intervalos de crescimento e decrescimento da função acima! Existem várias maneiras de fazer isso! Mas, o enunciado pede para usarmos algum recurso gráfico! Eu vou usar o geogebra para isso, você pode usar qualquer programa que consiga fazer o plot! Bora lá!

Passo 2

O gráfico de nossa função é

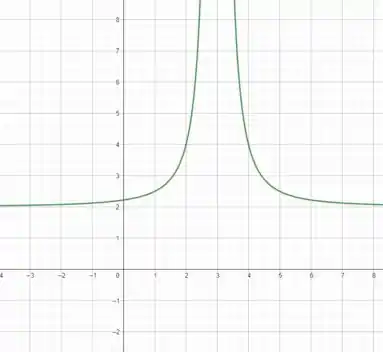
Note que a função cresce até divergir em x = 3 , valor em que o denominador de nossa função se anula, e portanto, não pertence ao nosso domínio, após x = 3 ela começa a decrescer para o que aparenta ser uma assíntota horizontal em g ( x ) = 2 . O intervalo de crescimento é

( - ∞ , 3 )

e, o intervalo de decrescimento

( 3 , + ∞ )

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

Crescimento: ( - ∞ , 3 ) e Decrescimento: ( 3 , + ∞ )

Exercícios de Livros Relacionados

Em uma investigação de assassinato, a temperatura do corpo era 32,5 ºC às 13h30 e 30,3 ºC uma hora depois. A temperatura normal do corpo é 37,0 ºC, e a temperatura do ambiente era 20 ºC. Quando o assa
Demonstre que quando x → ∞ , e x cresce mais rapidamente que x 2 para qualquer inteiro positivo, até mesmo x 1.000.000 . Dica: qual é enésima derivada de x n ?
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Mostre que 1 + x 31 + 1 3 x se x0 e confirme a d
53-54. Em cada parte, determine se a afirmação é verdadeira ou falsa. Se falsa, encontre funções para quais a afirmação não é válida.53. b) Se f e g forem crescentes em um intervalo, então f . g també
Nos Exercícios de 1 a 40, faça o seguinte: (a) ache os extremos relativos de f pelo teste da primeira derivada; (b) determine os valores de x nos quais os extremos relativos ocorrem; (c) determine os