UNICAMP – Cálculo 1 – Lista 1 – Questão 5.8Parte2
Faça alguns exemplos ilustrando o seguinte resultado: seja uma função contínua no intervalo .
Parte 2: Se para todo então será decrescente em
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa fazendo a seguinte afirmação
Se para todo então será decrescente em
o problema pede exemplos disso!
Para falar em exemplos, precisamos decifrar! Temos que
É a função derivada! Ela indica a taxa de crescimento ou decrescimento de uma função! Então quando a derivada de uma função é negativa em um certo intervalo, isso significa que a função é sim decrescente!
Agora vamos ver alguns exemplos disso?
Passo 2
Vamos considerar uma função exponencial com base menor do que zero
Sua derivada é
E sabemos que o domínio dessa função são todos os reais, então qualquer valor de que substituirmos na derivada resultará em um valor negativo
Beleza?
Vou começar por
Ok? E agora um número negativo, como
De qualquer forma temos uma derivada negativa! Pode ser que o valor da derivada seja menor, então a taxa de decrescimento é menor, mas ela segue decrescendo!
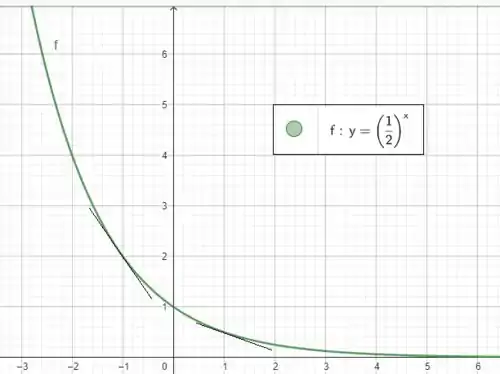
No gráfico estão representadas as duas retas tangentes nos pontos que vimos! A reta mais à esquerda tem uma inclinação maior, mas é uma inclinação negativa. Já a reta da direita é menos íngreme, indicando que ali a função está decrescendo a uma taxa menor!
Passo 3
Um outro exemplo é uma função linear do tipo
Derivando temos uma constante
E que é sempre um valor negativo, assim como a inclinação dessa curva!
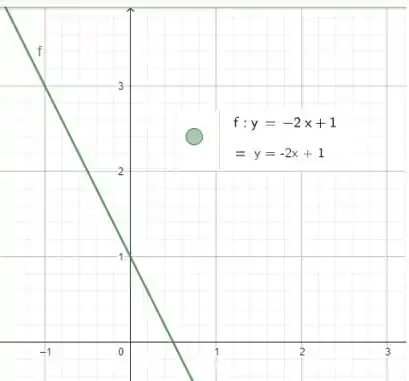
Beleza? Espero ter ajudado!
Até a próxima!