Determine:
Os intervalos nos quais é crescente.
Os intervalos nos quais é decrescente.
Passo 1
Para chegar nesses extremos precisamos derivar. Não precisamos nem transformar isso num polinômio e derivar, dá para usar a Regra do Produto:
Repara que dá para colocar em evidência um termo e dois termos :
Passo 2
Agora que já temos a derivada, para descobrir aonde essa função é crescente ou decrescente precisamos fazer um quadro de sinais com a derivada primeira:
Para construir esse quadro de sinais, é necessário avaliar cada termo dessa derivada. Por exemplo, para , sabemos que para qualquer valor de x maior que um, esse termo ficará negativo e para qualquer valor menor que 1, positivo.
Para , essa inversão de sinais ocorre em . Mas e para ? Nesse caso, para qualquer valor de x, o resultado será positivo, pois qualquer número ao quadrado é positivo e o número “1” que estamos somando também é!
Então, a nossa tabela de sinais fica assim:
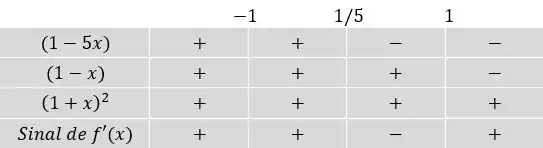
A última linha, sinal de , é obtida pela multiplicação das outras linhas. Como assim? Vamos olhar para a quarta coluna da tabela. Nessa coluna, multiplicando os sinais das três primeiras linhas (-, + e +), o resultado do produto dá negativo. Portanto, esse é o sinal da última linha (sinal de )!
Daí tiramos que a função cresce em todo o domínio, menos no intervalo , onde é, portanto, decrescente. Formalmente falando: