De os intervalos em que a função é crescente e em que é decrescente
Passo 1
Achando a primeira derivada
Quando a gente fala de teste de crescimento e decrescimento de função, o truque vai estar sempre na inclinação da reta tangente, não é mesmo? Se a inclinação é positiva, então a função cresce. Se é negativa, então a função decresce. Show, mas como a inclinação da reta tangente é dada pela derivada da função, a primeira coisa a fazer é derivar. Então, partiu:
Bem, então o que temos que fazer agora é estudar o sinal da primeira derivada, pois temos que lembrar da relação direta entre o sinal da derivada e da função:
Já que é sempre válido:
Passo 2
Para facilitar a nossa vida... Vamos colocar uma fração só na derivada...
- Se você se lembrar, o gráfico da função é bem famoso...
- é um gráfico parecido com esse, mas deslodado unidades para baixo...
- Como o sinal que buscamos analisar é a divisão dos dois sinais:
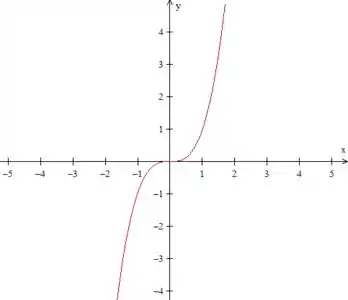
Onde o sinal de pode ser indicado assim:
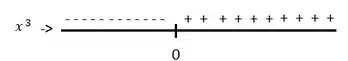
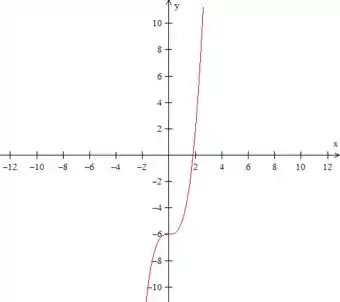
Que pode ser representado por:

Esse raiz cúbica é onde a é :
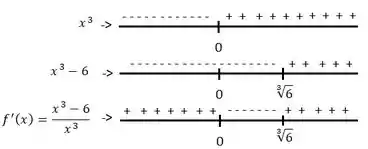
Passo 3
Analisando então somento os sinais da derivada:
![]()
Já que é sempre válido:
Podemos falar que