Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
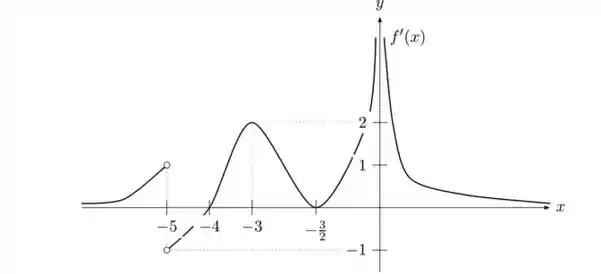
Responda, justificando, o que se pede:
Os intervalos onde é crescente, e onde é decrescente.
Passo 1
Fala galera, tudo bem com vocês?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Além disso, o enunciado também nos falou que:
Com essas informações precisamos determinar os intervalos em que é crescente, e os intervalos em que é decrescente.
A ideia é olharmos para a derivada de , se:
Então, vamos usar o gráfico dado para obter essa informação.
Passo 2
Vamos analisar o gráfico da derivada da função:
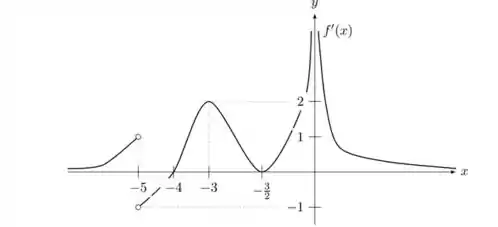
Primeiro vamos pesquisar os intervalos em que a função está crescendo. Ou seja, os trechos em que .
Temos:
E é isso! Esses são os intervalos em que a função cresce.
Já para a parte decrescente, devemos ver os intervalos em que . Ou seja:
Prontinho!
Pegaram a ideia? Obrigado pela atenção 😊
Resposta
crescente:
decrescente: