Considere a função cujo gráfico está representado abaixo. Determine os intervalos de crescimento e decrescimento de
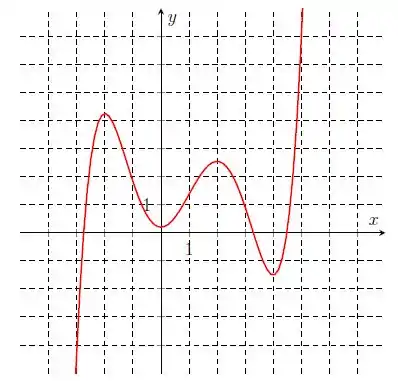
Passo 1
Fala aí, galeraaa!! O que é um intervalo com crescimento e decrescimento? É aquele onde a derivada é positiva e negativa, respectivamente. E conseguimos achar através do gráfico onde que:
Ou
Isso pode ser achado graficamente apenas analisando em que momentos a função “cresce” ou “decresce”, ou apenas, “sobe” ou “desce”.
Vamos então marcar de verde as partes crescentes e de azul as partes decrescentes, beleza?
Passo 2
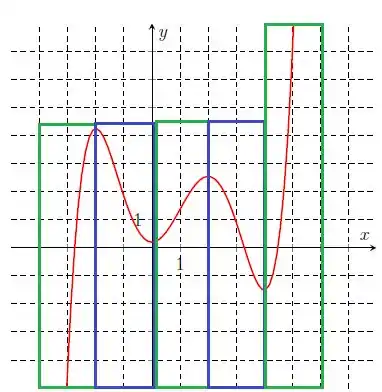
Resposta
Demonstração