UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profs, Emerson e Raimundo - Lista 5, Questão 1
Considere a função abaixo:
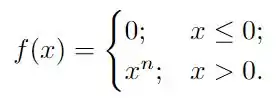
Onde é um número inteiro positivo. Para que valores de a função é derivável em ? Para que valores de a função é contínua em ?
Passo 1
Eaew, belezinha?
Precisamos avaliar a seguinte função
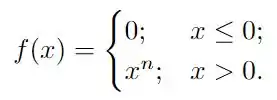
em que é um inteiro positivo, e identificar para quais valores de está função é derivável e para quais valores é uma função é contínua em . Vamos analisar as condições que estabelecem que uma função seja derivável em um ponto, assim como as condições para que ela seja contínua, e ver se isso vincula de alguma forma os valores possíveis de . Vamos lá!
Passo 2
Para verificar se a função é diferenciável é conveniente avaliarmos primeiro a sua continuidade, uma vez que, uma função que não pode ser diferenciável se não for contínua no ponto! A definição de continuidade é tal que
Note que quando , temos que a função é . Mas, como garantimos que o limite do lado direito existe? Precisamos calcular os limites laterais
e
ou seja, aproximar a função de por valores levemente menores (-) e por valores levemente maiores (+), note que para valores menores, nossa função é nula, portanto
e, para valores levemente maiores, temos que
contanto que , já que por definição. Sendo assim, contanto que , temos que a função é contínua em , já que
Vamos verificar a diferenciabilidade agora! Saca só!
Passo 3
Para que a função seja diferenciável em um ponto, precisamos que o seguinte limite exista
que pode ser simplificado já que a função é contínua em . O limite para valores levemente menores é tal que
já que a função é identicamente nula, agora, para valores levemente maiores, temos que
lembre que para ser contínua, agora, esta relação requer que , já que isso também nos levaria a , tomando que , temos que
Portanto, contanto que
a função será contínua e derivável! A questão foi isso! Te vejo na próxima! Tchau Tchau!