UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 2.2
(2) Encontre o volume comum de dois cilindros circulares, cada um com raio , se os eixos dos cilindros se intersectam em ângulos retos.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, nosso objetivo é calcular o volume entre dois cilindros de raio sendo que eles estão dispostos perpendicularmente com seus eixos centrais se cruzando.
Tem ideia de como fazer isso? 🤔
Para esse problema, temos que obter o cálculo do volume a partir da integral da área, ou seja
Primeiro vamos analisar como é essa região entre os dois cilindros e verificar como a área se comporta.
Sacou? Bora começar? 😉
Passo 2
Para esboçar essa região podemos esboçar um cilindro cujo eixo central é o eixo e outro no eixo , veja só
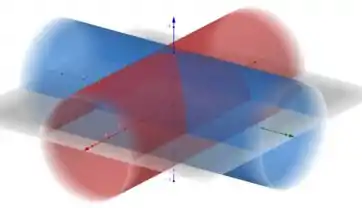
Cada seção transversal do sólido no plano perpendicular ao eixo é um quadrado, um quarto desse quadrado e um oitavo de é visto na figura abaixo:
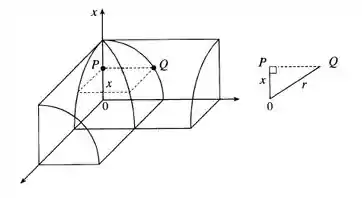
Temos pela figura que os limites de integração são e , e a área de um quarto de quadrado é dada pela expressão :
Pronto, agora só falta calcular o volume:
Tranquilo até aqui? 😬
Passo 3
Agora o que nos resta é calcular essa integral...
Pelo método de integração polinomial, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
