USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 3.19
Sejam cujos gráficos são:
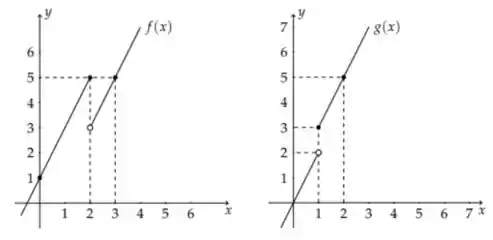
Então pode-se dizer que :
a) não é derivável somente em ;
b) não é derivável somente em ;
c) não é derivável somente em e ;
d) é derivável em todos os pontos e ;
e) é derivável em todos os pontos e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá dois gráficos de duas funções e e nos dá algumas alternativas a respeito da derivação de .
Para prosseguirmos, temos que entender que:
Agora vamos lá resolver!! 😉
Passo 2
Bom... a gente pode observar que, apesar das descontinuidades, as funções não sofrem alterações em suas inclinações, as quais permanecem constantes e iguais a .
Por consequência, as funções são consideradas deriváveis em todos os pontos e:
Assim, a alternativa correta é a letra e):
Entendeu direitinho? Responde aee ;)
Resposta
e) é derivável em todos os pontos e .